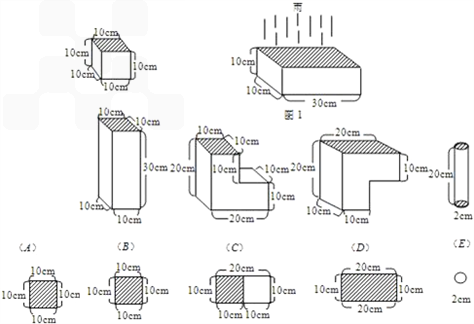
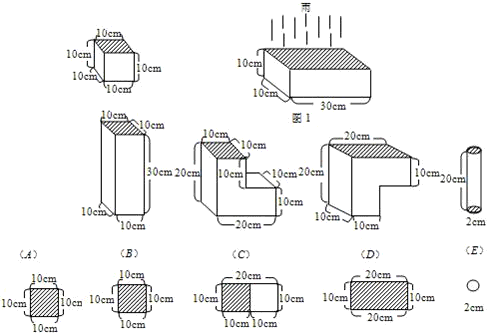
题目内容
雨哗哗地不停地下着,如在雨地里放一个如图1那样的长方体形状的容器,雨水将它下满要用1小时.有下列(A)-(E)不同的容器(图2),雨水下满各需多少时间?
(注:面是朝上的敞口部分.)
解:在例图所示的容器中,容积:接水面积=(10×10×30):(10×30)=10:1,需1小时接满,
所以:容器(A):容积:接水面积=(10×10×10):(10×10)=10:1,需1小时接满;
容器(B):容积:接水面积=(10×10×30):(10×10)=30:1,需3小时接满;
容器(C):容积:接水面积=(20×20×10-10×10×10):(10×10)=30:1,需3小时接满;
容器(D):容积:接水面积=(20×20×10-10×10×10):(20×10)=15:1,需1.5小时接满;
容器(E):容积:接水面积=20×S:S=20:1(S为底面积),接水时间为2小时.
分析:(1)图A只要根据容积公式“正方体的体积=棱长3”代入数字,然后求出容积和底面积(接水面积)的比,即可得出;
(2)图A只要根据容积公式“正方体的体积=棱长3”代入数字,然后求出容积和底面积(接水面积)的比,即可得出;
(3)图C把该图形理解为从一个长为20厘米,宽为10厘米,高为20厘米的长方体中减去了一个棱长为10厘米的正方体,根据长方体和正方体的体积公式,求出容积和底面积(接水面积)的比,即可得出;
(4)图D该图形理解为从一个长为20厘米,宽为10厘米,高为20厘米的长方体中减去了一个棱长为10厘米的正方体,根据长方体和正方体的体积公式,求出容积和底面积(接水面积)的比,即可得出;
(5)图E只要根据容积公式“圆柱是体积=底面积×高”,代入数字,求出容积和底面积(接水面积)的比,即可得出;
点评:此题做题的关键是:根据长方体、正方体及圆柱的体积公式进行计算即可.
所以:容器(A):容积:接水面积=(10×10×10):(10×10)=10:1,需1小时接满;
容器(B):容积:接水面积=(10×10×30):(10×10)=30:1,需3小时接满;
容器(C):容积:接水面积=(20×20×10-10×10×10):(10×10)=30:1,需3小时接满;
容器(D):容积:接水面积=(20×20×10-10×10×10):(20×10)=15:1,需1.5小时接满;
容器(E):容积:接水面积=20×S:S=20:1(S为底面积),接水时间为2小时.
分析:(1)图A只要根据容积公式“正方体的体积=棱长3”代入数字,然后求出容积和底面积(接水面积)的比,即可得出;
(2)图A只要根据容积公式“正方体的体积=棱长3”代入数字,然后求出容积和底面积(接水面积)的比,即可得出;
(3)图C把该图形理解为从一个长为20厘米,宽为10厘米,高为20厘米的长方体中减去了一个棱长为10厘米的正方体,根据长方体和正方体的体积公式,求出容积和底面积(接水面积)的比,即可得出;
(4)图D该图形理解为从一个长为20厘米,宽为10厘米,高为20厘米的长方体中减去了一个棱长为10厘米的正方体,根据长方体和正方体的体积公式,求出容积和底面积(接水面积)的比,即可得出;
(5)图E只要根据容积公式“圆柱是体积=底面积×高”,代入数字,求出容积和底面积(接水面积)的比,即可得出;
点评:此题做题的关键是:根据长方体、正方体及圆柱的体积公式进行计算即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 雨哗哗地不停地下着,如在雨中放着一个如图1那样的长方体的容器,雨水将它注满要1小时;如在雨中放着一个如图2那样的长方体的容器,雨水将它注满要
雨哗哗地不停地下着,如在雨中放着一个如图1那样的长方体的容器,雨水将它注满要1小时;如在雨中放着一个如图2那样的长方体的容器,雨水将它注满要
 面是朝上的敞口部分)
面是朝上的敞口部分)