题目内容
【题目】下面是用小正方体堆成的图形，现在把它的表面涂上色，共有（______）个小正方形不会被涂色。
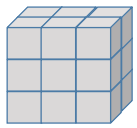
【答案】66
【解析】
根据正方体表面涂色的特点，分别得出切割后的小正方体涂色面的排列特点：（1）没有涂色的都在内部；（2）一面涂色的都在每个面上（除去棱上的小正方体）；（3）两面涂色的在每条棱上（除去顶点处的小正方体）；（4）三面涂色的在每个顶点处；由此得出有下面两种做法。
方法一：找没有被涂色的小正方形，就是找粘贴处。前后有9处，左右有12处，上下有12处，共33处。一共没有被涂色的小正方形：33×2＝66（个）
方法二：图形中除了没被涂色的小正方形就是涂色的，所以用总－染＝没染。
先算总面，用光头法数出3×6＝18个小正方体。总：18×6＝108（个）
再算染，前后：9×2＝18（个）；左右：6×2＝12（个）；上下：6×2＝12（个）。
染了的加起来：18＋12＋12＝42（个）没染：108－42＝66（个）
练习册系列答案
相关题目