题目内容
【题目】在一个8×8的方格棋盘的方格中,填入从1到64这64个数.问:是否一定能够找到两个相邻的方格,它们中所填数的差大于4?
【答案】不存在相邻数之差都不大于4的情况,即不论怎样填数必有相邻两数的差大于4
【解析】
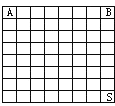
试题分析:考虑这个方格棋盘的左上角、右上角及右下角内的数A,B,S.设存在一个填数方案,使任意相邻两格中的数的差不大于4,考虑最大和最小的两个数1和64的填法,据此展开分析推理,即可解答问题.
解:为了使相邻数的差不大于4,最小数1和最大数的“距离”越大越好,即把它们填在对角的位置上(A=1,S=64);
然后,我们沿最上行和最右行来观察:因为相邻数不大于4,从 A→B→S共经过14格,
所以 S≤1+4×14=57(每次都增加最大数4),与S=64矛盾.
因而,1和64不能填在“最远”的位置上.
显然,1和64如果填在其他任意位置,那么从1到64之间的距离更近了,更要导致如上的矛盾.
因此,不存在相邻数之差都不大于4的情况,即不论怎样填数必有相邻两数的差大于4.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目