题目内容
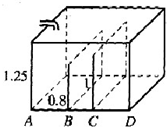 如图,一个长方体的水池水深1.25米,一个水龙头要注满水池需要3.5小时.现在要在水池内设置两块与池壁平行的挡板(体积忽略不计),一块高0.8米(B点),它挡成的区域恰好容纳1小时注水量,另一块高1米(C点),它挡成的区域恰好容纳2小时的注水量.那么AB、BC、CD这三段距离之比是多少?
如图,一个长方体的水池水深1.25米,一个水龙头要注满水池需要3.5小时.现在要在水池内设置两块与池壁平行的挡板(体积忽略不计),一块高0.8米(B点),它挡成的区域恰好容纳1小时注水量,另一块高1米(C点),它挡成的区域恰好容纳2小时的注水量.那么AB、BC、CD这三段距离之比是多少?分析:先设出AB、BC、CD部分的底面积分别为a、b、c,进而根据“体积=底面积×高”表示出各部分的体积:AB部分水的体积是0.8a,AC部分水的体积是(a+b)×1,因为每小时的水流量一定,列出等量关系,再求连比,0.8a÷1=(a+b)×1÷2,可得a:b=5:3,因为宽相等,即长度比也为5:3;
同理求出b:c=25:16,因为每小时的水流量一定,所以(a+b+c)×1.25÷3.5=0.8a÷1,进而可得:a:c=25:16,然后求abc的连比即可.
同理求出b:c=25:16,因为每小时的水流量一定,所以(a+b+c)×1.25÷3.5=0.8a÷1,进而可得:a:c=25:16,然后求abc的连比即可.
解答:解:设AB、BC、CD部分的底面积分别为a、b、c,
则AB部分水的体积是0.8a,AC部分水的体积是(a+b)×1,因为每小时的水流量一定,
所以:0.8a÷1=(a+b)×1÷2,
0.8a=0.5a+0.5b,
0.3a=0.5b,
a:b=5:3,
因为宽都相等,所以AB:BC=5:3;
同理:因为每小时的水流量一定,所以:
(a+b+c)×1.25÷3.5=0.8a÷1,
(a+0.6a+c)×1.25=0.8a×3.5,
(1.6a+c)×1.25=2.8a,
2a+1.25c=2.8a,
2.8a-2a=1.25c,
所以:a:c=25:16,
因为宽都相等,所以AB:CD=25:16;
因为AB:BC=5:3=25:15,所以AB:BC:CD=25:15:16;
答:AB、BC、CD这三段距离之比是25:15:16.
则AB部分水的体积是0.8a,AC部分水的体积是(a+b)×1,因为每小时的水流量一定,
所以:0.8a÷1=(a+b)×1÷2,
0.8a=0.5a+0.5b,
0.3a=0.5b,
a:b=5:3,
因为宽都相等,所以AB:BC=5:3;
同理:因为每小时的水流量一定,所以:
(a+b+c)×1.25÷3.5=0.8a÷1,
(a+0.6a+c)×1.25=0.8a×3.5,
(1.6a+c)×1.25=2.8a,
2a+1.25c=2.8a,
2.8a-2a=1.25c,
所以:a:c=25:16,
因为宽都相等,所以AB:CD=25:16;
因为AB:BC=5:3=25:15,所以AB:BC:CD=25:15:16;
答:AB、BC、CD这三段距离之比是25:15:16.
点评:此题较难,应认真分析,解答此题的关键是:设出AB、BC、CD部分的底面积,表示出各部分的体积,因为每小时的水流量一定,列出等量关系,分别求出AB和BC的比及AB和CD的比,进而求出这三条线段的连比.

练习册系列答案
相关题目
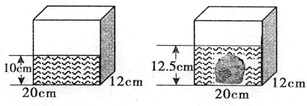 如图,一个长方体水槽里有一些水,把一块土豆放进去,土豆的体积是多少?
如图,一个长方体水槽里有一些水,把一块土豆放进去,土豆的体积是多少?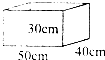 如图,一个无盖的长方体玻璃鱼缸,长50厘米,宽40厘米,高30厘米.
如图,一个无盖的长方体玻璃鱼缸,长50厘米,宽40厘米,高30厘米. 如图是一个长方体(图上所标数据均是从里面测量所得),请仔细观察,并解答下面各题.
如图是一个长方体(图上所标数据均是从里面测量所得),请仔细观察,并解答下面各题. 如图,一只装有水的圆柱形玻璃杯,底面积是80cm2,水深8cm.现将一个底面积是16cm2的长方体铁块竖放在水中后,仍有一部分铁块露在外面,现在水深多少厘米?
如图,一只装有水的圆柱形玻璃杯,底面积是80cm2,水深8cm.现将一个底面积是16cm2的长方体铁块竖放在水中后,仍有一部分铁块露在外面,现在水深多少厘米?


