Question

【题目】在三角形ABC中，一个锐角是30°，截取这个角后（如图所示），剩下图形的内角和是多少度？

Answer 1

【答案】360°

【解析】

根据三角形的内角和解答，该三角形被一条直线所截，产生了四个新的角，通过三角形的内角和为180°，其中一个角为直角，可求出被截小三角形的一个内角，利用该内角和∠ADF组成平角，计算出∠ADF的度数。再次利用三角形的内角和是180°可求出∠A＋∠C的和，再将∠ADC＋∠DFC（已知）＋∠A＋∠C便可求出剩下图形的内角和。

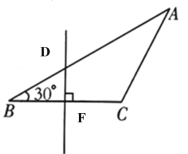
∠BAC＋∠ACB＝180°－30°＝150°

∠DFC＝∠DFB＝90°

∠BDF＝180°－90°－30°＝60°

∠ADF＝180°－60°＝120°

∠ADF＋∠DFC＋∠BAC＋∠ACB＝150°＋90°＋120°＝360°

答：剩下图形的内角和是360°。