题目内容
三项连比的性质是:
如果a:b=m:n,b:c=n:k,那么a:b:c=
如果k≠0,那么a:b:c=ak:
:
如果a:b=m:n,b:c=n:k,那么a:b:c=
m:n:k
m:n:k
.如果k≠0,那么a:b:c=ak:
k2
k2
=| a | k |
1
1
.分析:(1)把“a:b=m:n”理解为a是b的
,“b:c=n:k”理解为c是b的
,进而根据题意进行比即可.
(2)依据比例的基本性质,即两内项之积等于两外项之积,即可得解.
| m |
| n |
| k |
| n |
(2)依据比例的基本性质,即两内项之积等于两外项之积,即可得解.
解答:解:(1)假设b是“1”,则a是
,c是
,
所以a:b:c=
:1:
=m:n:k;
(2)如果k≠0,那么a:b:c=ak:k2=
:1.
故答案为:m:n:k、k2、1.
| m |
| n |
| k |
| n |
所以a:b:c=
| m |
| n |
| k |
| n |
(2)如果k≠0,那么a:b:c=ak:k2=
| a |
| k |
故答案为:m:n:k、k2、1.
点评:解答此题的关键:把比转化为分数,在同一单位“1”下进行比,进而得出结论.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
比最大的三位数多
100的数是[
]|
A .199 |
B .1909 |
C .1099 |
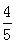 ,如果后项乘4,前项不变,求新的比值,列式是
,如果后项乘4,前项不变,求新的比值,列式是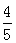 ×4
×4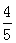 ÷4
÷4 和1吨铁的
和1吨铁的 一样重。
一样重。 ,如果比的后项乘2,要使比值仍是
,如果比的后项乘2,要使比值仍是 ,那么比的前项也应乘2。
,那么比的前项也应乘2。