题目内容
(2010?哈尔滨模拟)如果两个不同的长方形周长相同,长宽的比分别是5:4与15:13,那么它们的面积比是
3136:3159
3136:3159
.分析:设两个长方形周长都是a,根据长方形的周长计算方法求出长方形一条长和宽的和,进而根据按比例分配知识,分别求出第一个长方形的长、宽及第二个长方形的长、宽,然后根据长方形的面积计算方法分别求出两个长方形的面积,然后用第一个长方形的面积与第二个长方形的面积相比即可.
解答:解:设两个长方形周长都是a,则:
5+4=9(份),
15+13=28(份),
(a÷2×
)×(a÷2×
),
=
a×
a,
=
a2,
(a÷2×
)×(a÷2×
),
=
a×
a,
=
a2,
a2:
a2=
:
=
×
=3136:3159;
答:面积之比为3136:3159.
故答案为:3136:3159.
5+4=9(份),
15+13=28(份),
(a÷2×
| 5 |
| 9 |
| 4 |
| 9 |
=
| 5 |
| 18 |
| 2 |
| 9 |
=
| 5 |
| 81 |
(a÷2×
| 15 |
| 28 |
| 13 |
| 28 |
=
| 15 |
| 56 |
| 13 |
| 56 |
=
| 195 |
| 3136 |
| 5 |
| 81 |
| 195 |
| 3136 |
| 5 |
| 81 |
| 195 |
| 3136 |
| 5 |
| 81 |
| 3136 |
| 195 |
答:面积之比为3136:3159.
故答案为:3136:3159.
点评:解答此题还可以设一个长方形的长为5X,则宽为4X,另一个长方形的长为15Y,则宽为13Y,由周长相等得:2×(5X+4X)=2(15Y+13Y),所以X=
,那么它们的面积比为(5X×4X):(15Y×13Y)=3136:3159.
| 28Y |
| 9 |

练习册系列答案
相关题目
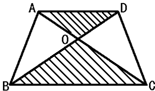 (2010?哈尔滨模拟)如图,已知梯形ABCD中AD=
(2010?哈尔滨模拟)如图,已知梯形ABCD中AD=