题目内容
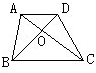
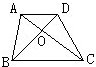 图中△AOB的面积为18cm2,线段OB的长度为OD的3倍,则梯形ABCD的面积
图中△AOB的面积为18cm2,线段OB的长度为OD的3倍,则梯形ABCD的面积为
96平方厘米
96平方厘米
.分析:要求梯形ABCD的面积可以将它分成两部分来求,即:求出△ABD与△BDC的面积.
(1)△ABD的面积:因为线段OB的长度为OD的3倍,所以BD=
BO,所以△ABD的面积=
△AOB的面积=
=24平方厘米,
(2)△BDC的面积:梯形中△AOD与△BOC相似,AD:BC=OD:OB=1:3,因为△ABD与△BDC的高相同,所以△ABD与△BDC的面积比为1:3,由此可得△BDC的面积为:24×3=72平方厘米.
由上述计算即可得出梯形ABCD的面积.
(1)△ABD的面积:因为线段OB的长度为OD的3倍,所以BD=
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
(2)△BDC的面积:梯形中△AOD与△BOC相似,AD:BC=OD:OB=1:3,因为△ABD与△BDC的高相同,所以△ABD与△BDC的面积比为1:3,由此可得△BDC的面积为:24×3=72平方厘米.
由上述计算即可得出梯形ABCD的面积.
解答:解:根据题干可得:BD=
BO,
△ABD的面积:
=24(平方厘米),
AD:BC=OD:OB=1:3,因为△ABD与△BDC的高相同,所以△ABD与△BDC的面积比为:1:3,
则△BDC的面积为:24×3=72(平方厘米),
24+72=96(平方厘米),
答:这个梯形的面积是96平方米.
故答案为:96平方厘米.
| 4 |
| 3 |
△ABD的面积:
| 4 |
| 3 |
AD:BC=OD:OB=1:3,因为△ABD与△BDC的高相同,所以△ABD与△BDC的面积比为:1:3,
则△BDC的面积为:24×3=72(平方厘米),
24+72=96(平方厘米),
答:这个梯形的面积是96平方米.
故答案为:96平方厘米.
点评:此题利用三角形相似的性质求出图形中线段的比,从而得出对应三角形面积的比,这是计算图形面积时常用的一种手段.

练习册系列答案
相关题目
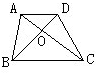
 如图:扇形OAB的半径为lOcm,∠AOB=90°分别以OA、OB为直径作半圆,两半圆相交于点C.求图中阴影部分面积是多少?
如图:扇形OAB的半径为lOcm,∠AOB=90°分别以OA、OB为直径作半圆,两半圆相交于点C.求图中阴影部分面积是多少?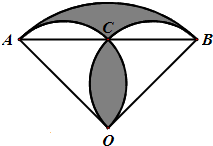 如图:扇形OAB的半径为lOcm,∠AOB=90°分别以OA、OB为直径作半圆,两半圆相交于点C.求图中阴影部分面积是多少?
如图:扇形OAB的半径为lOcm,∠AOB=90°分别以OA、OB为直径作半圆,两半圆相交于点C.求图中阴影部分面积是多少?