题目内容
【题目】 ①如图,O是直线上的一点,请过O点画出已知直线的垂线.
②以O为圆心画一个半径是2厘米的圆.
③在圆中画出一个最大的正方形,剩下的部分用阴影表示.
④计算这个阴影部分的面积.
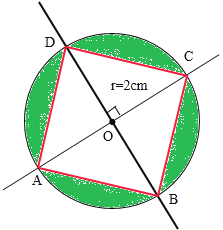
【答案】如图,面积是4.56平方厘米
【解析】
试题分析:(1)过直线上一点画这条直线的垂线:让三角板的直角顶点落在给定的O点上.把三角板的一条直角边与这条直线重合,沿着另一条直角边画出的直线就是前一条直线的垂线(直角顶点是垂足);
(2)以O为圆心,以2厘米为半径即可画出符合要求的圆;
(3)依次连接已知直线及其垂线与圆的4个交点,所得到的四边形就是这个圆中最大的正方形,然后将剩余部分标上阴影即可.
(4)阴影部分的面积=圆的面积﹣正方形的面积,因为正方形的对角线等于圆的直径,于是即可分别利用圆和正方形的面积公式求解.
解:据(1)、(2)、(3)的分析画图如下:
 ;
;
阴影部分的面积:
3.14×22﹣2×2×2÷2×2,
=12.56﹣8,
=4.56(平方厘米);
答:阴影部分的面积是4.56平方厘米.

练习册系列答案
相关题目
