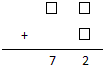题目内容
10.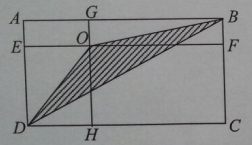 如图,在长方形ABCD内,直线EF与AB边平行,GH与BC边平行,AB与GH相交于O点,已知AG=5厘米,AE=2厘米,FC=6厘米,HC=10厘米,那么三角形BOD的面积是25平方厘米.
如图,在长方形ABCD内,直线EF与AB边平行,GH与BC边平行,AB与GH相交于O点,已知AG=5厘米,AE=2厘米,FC=6厘米,HC=10厘米,那么三角形BOD的面积是25平方厘米.
分析 由条件可知:DH=AG=5厘米,FO=HC=10厘米,BF=AE=2厘米,DC=DH+HC=5厘米+10厘米=15厘米,BC=BF+FC=2厘米+6厘米=8厘米,要求的三角形BOD的面积=三角形BOF的面积+三角形DOH的面积+长方形OHCF的面积-三角形DBC的面积,据此解答即可.
解答 解:因为长方形ABCD中,
直线EF与AB边平行,GH与BC边平行
所以DH=AG=5厘米
FO=HC=10厘米
BF=AE=2厘米
DC=DH+HC=5厘米+10厘米=15厘米
BC=BF+FC=2厘米+6厘米=8厘米
三角形BOD的面积=三角形BOF的面积+三角形DOH的面积+长方形OHCF的面积-三角形DBC的面积
=10×2÷2+5×6÷2+10×6-15×8÷2
=10+15+60-60
=25(平方厘米)
答:三角形BOD的面积是25平方厘米.
故答案为:25平方厘米.
点评 本题解答的关键是:求阴影面积利用间接方法,这是数学上的重要的方法.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
1.求制作一个鱼缸所需的材料是求鱼缸的( )
| A. | 棱长和 | B. | 是求表面积 | C. | 求容积 | D. | 求体积 |