题目内容
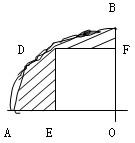 如下图,正方形DEOF在四分之一圆中,圆的半径为10 厘米.
如下图,正方形DEOF在四分之一圆中,圆的半径为10 厘米.(1)画出这个图形的对称轴; (2)图中阴影面积是多少?
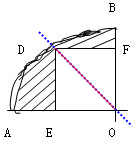
分析:连接OD,即正方形DEOF的对角线,也是这个圆的一条半径,再依据轴对称图形的意义,则OD所在的直线就是这个图形的对称轴,然后根据“正方形的面积=对角线×对角线×12,”算出正方形的面积,再根据“四分之一圆的面积=
×πr2“算出这个四分之一圆的面积,最后用四分之一圆的面积减去正方形的面积,就是阴影部分的面积.
| 1 |
| 4 |
解答:解:如图,OD所在的直线就是这个图形的对称轴,
正方形的面积=对角线×对角线×
,
=10×10×
,
=50(平方厘米);
四分之一圆的面积=
×πr2,
=
×3.14×102,
=78.5(平方厘米)
阴影部分的面积:78.5-50=28.5(平方厘米)
答:阴影部分的面积是28.5平方厘米.

正方形的面积=对角线×对角线×
| 1 |
| 2 |
=10×10×
| 1 |
| 2 |
=50(平方厘米);
四分之一圆的面积=
| 1 |
| 4 |
=
| 1 |
| 4 |
=78.5(平方厘米)
阴影部分的面积:78.5-50=28.5(平方厘米)
答:阴影部分的面积是28.5平方厘米.
点评:在这道题中首先分析阴影部分是用什么图形减去什么图形得到的;另外在这里的正方形的面积直接根据对角线去求.

练习册系列答案
相关题目
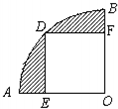 如右图,正方形DEOF在四分之一圆中,如果圆的半径为1厘米,那么,阴影部分的面积是
如右图,正方形DEOF在四分之一圆中,如果圆的半径为1厘米,那么,阴影部分的面积是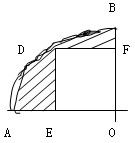 如下图,正方形DEOF在四分之一圆中,圆的半径为10 厘米.
如下图,正方形DEOF在四分之一圆中,圆的半径为10 厘米.