题目内容
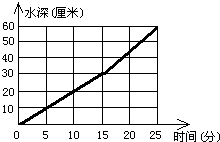 (2007?南长区)在一个长100厘米、宽80厘米、高100厘米的长方体水箱中有A、B两个进水管,先开A管,经过一段时间后两管齐开.下面折线统计图表示进水情况,请根据图回答问题.
(2007?南长区)在一个长100厘米、宽80厘米、高100厘米的长方体水箱中有A、B两个进水管,先开A管,经过一段时间后两管齐开.下面折线统计图表示进水情况,请根据图回答问题.(1)A管开放
15
15
分钟后,B管才开放与A管同时进水;B管开始进水时,水箱中的水深30
30
厘米.(2)A管每分钟进水
16000
16000
毫升.(3)A、B两管同时进水,每分钟进水
24000
24000
毫升.分析:(1)从折线统计图中可以看出,在A管开放15分钟后,折线上升幅度增大,说明B管是在A管开放15分钟后才开始进水的;B管开始进水时水箱内水深30厘米;
(2)可利用长方体的体积公式底面积×高确定A管15分钟进水的体积,然后再用水的体积除以水的深度即是A管每分钟进水的速度;
(3)A、B两管在(25-15)分钟内注入了(60-30)厘米深的水,可用(60-30)厘米深的水的体积除以A、B同时放入水的时间即可得到A、B两管同时进水的速度.
(2)可利用长方体的体积公式底面积×高确定A管15分钟进水的体积,然后再用水的体积除以水的深度即是A管每分钟进水的速度;
(3)A、B两管在(25-15)分钟内注入了(60-30)厘米深的水,可用(60-30)厘米深的水的体积除以A、B同时放入水的时间即可得到A、B两管同时进水的速度.
解答:解:(1)60-30=30(厘米),
答:A管开放15分钟后,B管才开放与A管同时进水;B管开始进水时,水箱内水深30厘米;
(2)(100×80×30)÷15
=240000÷15,
=16000(毫升),
答:A管每分钟进水16000毫升;
(3)[100×80×(60-30)]÷(25-15)
=[8000×30]÷10,
=240000÷10,
=24000(毫升),
答:A、B两管同时进水,每分钟进水24000毫升.
故答案为:(1)15,30,(2)16000,(3)24000.
答:A管开放15分钟后,B管才开放与A管同时进水;B管开始进水时,水箱内水深30厘米;
(2)(100×80×30)÷15
=240000÷15,
=16000(毫升),
答:A管每分钟进水16000毫升;
(3)[100×80×(60-30)]÷(25-15)
=[8000×30]÷10,
=240000÷10,
=24000(毫升),
答:A、B两管同时进水,每分钟进水24000毫升.
故答案为:(1)15,30,(2)16000,(3)24000.
点评:此题的关键是根据统计图确定相应时间内对应的水的深度及根据长方体的体积公式计算出水的体积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2007?南长区)母亲节时,小明送妈妈一只茶杯.(如图)
(2007?南长区)母亲节时,小明送妈妈一只茶杯.(如图)