题目内容
 请将下图分成3个小三角形,使得三个小三角形的面积比是1:2:3,如果这个大三角形的面积是216cm2,那这3个小三角形的面积分别是多少?(保留作图痕迹)
请将下图分成3个小三角形,使得三个小三角形的面积比是1:2:3,如果这个大三角形的面积是216cm2,那这3个小三角形的面积分别是多少?(保留作图痕迹)
解:据分析画图如下:
 ,
,
1+2+3=6,
216× =36(平方厘米),
=36(平方厘米),
216× =72(平方厘米),
=72(平方厘米),
216-36-72=108(平方厘米),
答:这3个小三角形的面积分别是36平方厘米、72平方厘米和108平方厘米.
分析:因为等高不等底的三角形的面积比就等于对应底边的比,所以将三角形的一条底边,按照1:2:3分割,再将分割点分别于对应顶点连接,所得到的三角形的面积比就是1:2:3,再按照按比例分配的方法,即可求出它们的面积.
点评:解答此题的主要依据是:等高不等底的三角形的面积比就等于对应底边的比;按比例分配的方法解答.
 ,
,1+2+3=6,
216×
 =36(平方厘米),
=36(平方厘米),216×
 =72(平方厘米),
=72(平方厘米),216-36-72=108(平方厘米),
答:这3个小三角形的面积分别是36平方厘米、72平方厘米和108平方厘米.
分析:因为等高不等底的三角形的面积比就等于对应底边的比,所以将三角形的一条底边,按照1:2:3分割,再将分割点分别于对应顶点连接,所得到的三角形的面积比就是1:2:3,再按照按比例分配的方法,即可求出它们的面积.
点评:解答此题的主要依据是:等高不等底的三角形的面积比就等于对应底边的比;按比例分配的方法解答.

练习册系列答案
相关题目
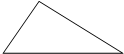 请将下图分成3个小三角形,使得三个小三角形的面积比是1:2:3,如果这个大三角形的面积是216cm2,那这3个小三角形的面积分别是多少?(保留作图痕迹)
请将下图分成3个小三角形,使得三个小三角形的面积比是1:2:3,如果这个大三角形的面积是216cm2,那这3个小三角形的面积分别是多少?(保留作图痕迹)