题目内容
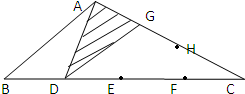 在三角形ABC中,如图:BD=DE=EF=FC,AG=GH=HC.已知阴影部分的面积是20平方厘米,那么三角形ABC的面积是
在三角形ABC中,如图:BD=DE=EF=FC,AG=GH=HC.已知阴影部分的面积是20平方厘米,那么三角形ABC的面积是80
80
平方厘米.分析:我们由△ADG的面积20平方厘米求出△ADC的面积,再由△ADC的面积占△ABC的面积的分率求出△ABC的面积.
解答:解:画图如下:
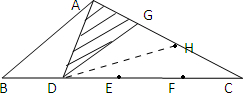
因为AG=GH=HC,
所以△AGD,△GDH,△CHD的面积相等都是20平方厘米,
所以△ADC的面积就是20×3=60(平方厘米);
再由下图可知:
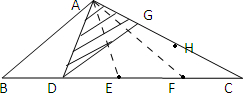
因为:BD=DE=EF=FC,
所以△ADC的面积是△ABC的
,
60÷
=60×
=80(平方厘米);
答:三角形ABC的面积是80平方厘米.
故答案为:80.

因为AG=GH=HC,
所以△AGD,△GDH,△CHD的面积相等都是20平方厘米,
所以△ADC的面积就是20×3=60(平方厘米);
再由下图可知:

因为:BD=DE=EF=FC,
所以△ADC的面积是△ABC的
| 3 |
| 4 |
60÷
| 3 |
| 4 |
| 4 |
| 3 |
答:三角形ABC的面积是80平方厘米.
故答案为:80.
点评:本题是一道简单的面积组合题,考查了三角形的面积与底的正比关系,考查了学生的应变及解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在三角形ABC中,BE=EF=FC,ED=2DA,求阴影部分的面积是三角形ABC面积的几分之几?
如图,在三角形ABC中,BE=EF=FC,ED=2DA,求阴影部分的面积是三角形ABC面积的几分之几? 如图,在三角形ABC中,BD=DC,AA1=
如图,在三角形ABC中,BD=DC,AA1=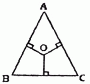 如图,在三角形ABC中有一点O,O点到三条边的垂线长都是2厘米,又知道三角形的周长是20厘米,那么三角形ABC的面积是
如图,在三角形ABC中有一点O,O点到三条边的垂线长都是2厘米,又知道三角形的周长是20厘米,那么三角形ABC的面积是 在三角形ABC中,如图:BD=DE=EF=FC,AG=GH=HC.已知阴影部分的面积是20平方厘米,那么三角形ABC的面积是________平方厘米.
在三角形ABC中,如图:BD=DE=EF=FC,AG=GH=HC.已知阴影部分的面积是20平方厘米,那么三角形ABC的面积是________平方厘米.