Question

计算探究题：探究多边形边数与内角和的关系．
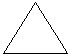
三角形内角和为180度，通过画辅助线方法，求多边形内角和度数． 
（1）你发现，若把边数看作n，则n边形的内角和用含有n的式子表示是

（n-2）?180°

．
（2）照这样计算，10边形的内角和是

1440

度．内角和为900度的多边形是

7

边形．

Answer 1

分析：（1）根据过同一顶点作出的对角线把多边形分成的三角形的个数的规律，再利用三角形的内角和等于180°即可推出多边形的内角和公式；
（2）根据前面推出的公式代入计算即可求解．

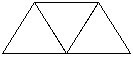
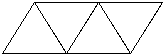
解答：解：（1）n边形分成（n-2）个三角形，
故n边形的内角和用含有n的式子表示是（n-2）?180°．

（2）10边形的内角和是（10-2）×180°=1440°，
900°÷180°+2
=5+2
=7．
答：10边形的内角和是 1440度．内角和为900度的多边形是 7边形．
故答案为：（n-2）?180°；1440，7．

点评：本题考查了多边形的内角和公式的推导，理清过同一个顶点把多边形分成的三角形的个数是解题的关键，也是本题的难点．