题目内容
【题目】(7分)如图:长方形ABCD中,AB=10厘米,BC=15厘米,E、F分别是所在边的中点.求阴影部分的面积.

【答案】答:阴影部分的面积是50平方厘米
【解析】
试题分析:如图所示,假设BD交AE与H点,AF交DB与G点,因为BF与AD平行,并且等于AD的![]() ,所以BG:GD=BE:AD=1:2,则BG:BD=1:3,同样的方法可以得出:DH:BD=1:3,所以BG=DH=
,所以BG:GD=BE:AD=1:2,则BG:BD=1:3,同样的方法可以得出:DH:BD=1:3,所以BG=DH=![]() BD,所以BG=GH=HD,所以△ABG与△AGH的面积相等,△ABG的面积+△BGF的面积=△AGH的面积+△BGE的面积,△AGH的面积+△BGE的面积=△ABE的面积,利用三角形的面积公式即可求解;又因△DFH的DF边上的高=
BD,所以BG=GH=HD,所以△ABG与△AGH的面积相等,△ABG的面积+△BGF的面积=△AGH的面积+△BGE的面积,△AGH的面积+△BGE的面积=△ABE的面积,利用三角形的面积公式即可求解;又因△DFH的DF边上的高=![]() BC,从而可以求其面积,据此即可求解.
BC,从而可以求其面积,据此即可求解.
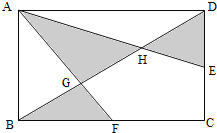
解:假设BD交AF与G点,AE交DB与H点,因为BF与AD平行,并且等于AD的![]() ,
,
所以BG:GD=BF:AD=1:2,则BG:BD=1:3,
同样的方法可以得出:DH:BD=1:3,
所以BG=DH=![]() BD,所以BG=GH=HD,
BD,所以BG=GH=HD,
所以△ABG与△AGH的面积相等,
△ABG的面积+△BGF的面积=△AGH的面积+△BGF的面积,
△AGH的面积+△BGF的面积=△ABF的面积=![]() ×10×
×10×![]() =
=![]() (平方厘米);
(平方厘米);
又因△DEH的DE边上的高=![]() ×15=5(厘米),
×15=5(厘米),
所以△DEH面积=![]() ×
×![]() ×5=
×5=![]() (平方厘米);
(平方厘米);
即阴影部分面积=![]() +
+![]() =50(平方厘米).
=50(平方厘米).
答:阴影部分的面积是50平方厘米.

练习册系列答案
相关题目