题目内容
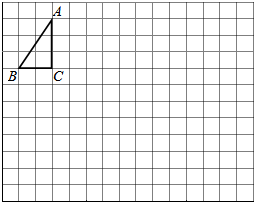
13. 如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.
如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.(1)将直角三角形纸板ABC绕三角形的边所在的直线旋转一周,能得到3种大小不同的几何体;
(2)分别计算绕三角形直角边所在的直线旋转一周,得到几何体的体积.(π取3)
分析 (1)将直角三角形纸板ABC绕三角形的三条边所在的直线旋转一周,能得到3种大小不同的几何体.
(2)如果以AB所在的直线旋转一周得到的圆锥的底面半径是8厘米,高是4厘米;如果以BC所在的直线旋转一周得到的圆锥的底面半径是4厘米,高是8厘米,根据圆锥的体积公式:v=$\frac{1}{3}$sh,把数据代入公式解答.
解答 解:(1)将直角三角形纸板ABC绕三角形的三条边所在的直线旋转一周,能得到3种大小不同的几何体.
(2)以AB为轴:
$\frac{1}{3}×3×{8}^{2}×4$
=$\frac{1}{3}×3×64×4$
=256(立方厘米);
以BC为轴:
$\frac{1}{3}×3×{4}^{2}×8$
=$\frac{1}{3}×3×16×8$
=128(立方厘米);
答:以AB为轴得到的圆锥的体积是256立方厘米,以BC为轴得到的圆锥的体积是128立方厘米.
故答案为:3.
点评 此题考查的目的是理解掌握圆锥的特征,以及圆锥体积公式的灵活运用.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 实践操作
实践操作