题目内容
17．
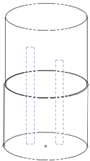如图，两根铁棒直立于桶底水平的木桶中，在桶中加水之后，一根漏出水面的长度是它的$\frac{1}{3}$，另一根露出水面的长度是它的$\frac{2}{5}$，已知两根铁棒的长度之和为38cm，那么两根铁棒露出水面之和为14cm．
分析 设水深为x厘米，则第一根的长度为x÷（1-$\frac{1}{3}$）厘米，第二根的长度为x÷（1-$\frac{2}{5}$）厘米，根据两根铁棒的长度之和为38厘米，列出方程解出x的值，进而求出两根铁棒露出水面的长度之和．
解答 解：设水深为x厘米，则第一根的长度为x÷（1-$\frac{1}{3}$）厘米，第二根的长度为x÷（1-$\frac{2}{5}$）厘米，根据题意得：
x÷（1-$\frac{1}{3}$）+x÷（1-$\frac{2}{5}$）=38
$\frac{3}{2}$x+$\frac{5}{3}$x=38
$\frac{19}{6}$x=38
x=12
12÷（1-$\frac{1}{3}$）×$\frac{1}{3}$+12÷（1-$\frac{2}{5}$）×$\frac{2}{5}$
=12$÷\frac{2}{3}$×$\frac{1}{3}$+12$÷\frac{3}{5}$×$\frac{2}{5}$
=6+8
=14（厘米）
答：两根铁棒露出水面之和为14厘米．
故答案为：14．
点评 解答本题的关键抓住水深相同这一条件，根据两根铁棒的长度之和为38厘米，列出方程解答即可．
练习册系列答案
名校课堂系列答案
相关题目
5．有两块面积相等的白铁皮和黑铁皮，白铁皮用去$\frac{2}{3}$平方米，黑铁皮用去$\frac{2}{3}$，剩下的白铁皮比黑铁皮面积大，那么原来两块铁皮的面积（ ）
| A． | 都小于1平方米 | B． | 都等于1平方米 | C． | 都大于1平方米 |
2．计算题
| 28-$\frac{4}{5}$-$\frac{1}{5}$= | 2÷1$\frac{1}{3}$+2×$\frac{1}{3}$= | $\frac{4}{5}$×2.5×8= | 80%×1.25×4= |
| $\frac{1}{3}$×24÷$\frac{1}{3}$= | [（$\frac{8}{9}$+1$\frac{1}{3}$ ）×$\frac{3}{4}$-0.75]÷$\frac{1}{12}$= | 85×0.75+15×75%= | $\frac{3}{8}$×（$\frac{7}{8}$+$\frac{1}{6}$）÷$\frac{3}{4}$= |
| $\frac{9}{10}$×（$\frac{5}{6}$-$\frac{2}{3}$）÷$\frac{13}{25}$= | $\frac{1}{8}$×5.25+3.75÷8+$\frac{1}{8}$= |
7．某企业2013年的产值如表：
（1）既要直观反映出这个企业每个季度的产值是多少，又要反映出产值的增长变化情况应绘制折线统计图
（2）平均每个季度产值多少万元？第二季度比第一季度增产百分之几？
（1）既要直观反映出这个企业每个季度的产值是多少，又要反映出产值的增长变化情况应绘制折线统计图
（2）平均每个季度产值多少万元？第二季度比第一季度增产百分之几？
| 季度 | 一 | 二 | 三 | 四 |
| 产值（万元） | 500 | 700 | 810 | 840 |