题目内容
17.从底面半径分别是3分米和5分米的等高圆锥形容器A和圆柱形容器B各一个,将容器A六次装满水后全部倒入容器B中,容器B的水深比容器高的60%还多6分米.填空回答问题:
(1)容器装满水一次倒入容器后,水深是容器高的12%
(2)容器A的容积是多少升?
分析 (1)首先根据圆柱、圆锥的体积公式,判断出容器A、容器B的体积的关系,即可判断出容器A装满水一次倒入容器B后,水深是容器B高的百分之几.
(2)首先根据容器A、容器B的体积的关系,以及容器B的水深比容器B高的60%还多6分米,求出两个容器的高是多少分米;最后根据圆锥的体积公式,求出容器A的容积是多少升即可.
解答 解:(1)因为圆锥形容器A、圆柱形容器B底面半径分别是3分米和5分米,
所以容器A的体积是容器B的体积的:
$\frac{{3}^{2}}{{5}^{2}}×\frac{1}{3}=\frac{9}{25}×\frac{1}{3}=\frac{3}{25}$=12%,
所以容器A装满水一次倒入容器B后,水深是容器高的12%.
答:容器A装满水一次倒入容器B后,水深是容器高的12%.
(2)容器A的高是:
6÷(12%×6-60%)
=6÷12%
=50(分米)
$\frac{1}{3}$×3.14×32×50
=$\frac{1}{3}×9×3.14×50$
=3×3.14×50
=471(升)
答:容器A的容积是471升.
故答案为:12.
点评 此题主要考查了圆柱、圆锥的体积的求法,要熟练掌握,解答此题的关键是求出两个容器的高是多少.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.图是一个正方体纸盒的展开图,那么和6号面相对的是( )号面.
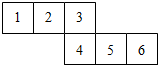

| A. | 1号 | B. | 2号 | C. | 3号 | D. | 4号 |
