题目内容
 如图的圆周上放置有3000枚棋子,按顺时针依次编号为1,2,3,…,2999,3000.首先取走3号棋子,然后按顺时针方向,每隔2枚棋子就取走1枚棋子,…,直到1号棋子被取走为止.问:此时,
如图的圆周上放置有3000枚棋子,按顺时针依次编号为1,2,3,…,2999,3000.首先取走3号棋子,然后按顺时针方向,每隔2枚棋子就取走1枚棋子,…,直到1号棋子被取走为止.问:此时,(1)圆周上还有多少枚棋子?
(2)在圆周上剩下的棋子中,从编号最小一枚棋子开始数,第181枚棋子的编号是多少?
分析:第一圈刚好把能被3整除的取走,即第一圈最后取走编号为3000的,共取走1000枚,剩下2000枚,此时1号仍为第一个.再从这2000枚棋子中隔2隔取走1个,第二圈最后取走的是2000枚中的第1998枚,共取走666枚,第1999、2000枚没有取走.再取就是第1号了,取走第1号时1000+666+1=1667枚棋子,还剩下1333枚棋子.
将第一圈取走的用绿色表示,将第二圈取走的用红色数字表示:

可见,每18个一循环,18个数去掉10个,剩下8个.拿走1后,剩下的最小编号是2,从2数第181枚,就是从1数第182枚.182÷8=22余6,22×18=396.
将396以后的数排列出来,并根据上述分析标上颜色:
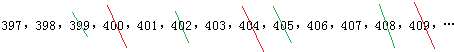
可见,剩下的第6个数是407,即取走1号棋子后,从剩下的最小号数,第181枚棋子的编号是407.
将第一圈取走的用绿色表示,将第二圈取走的用红色数字表示:

可见,每18个一循环,18个数去掉10个,剩下8个.拿走1后,剩下的最小编号是2,从2数第181枚,就是从1数第182枚.182÷8=22余6,22×18=396.
将396以后的数排列出来,并根据上述分析标上颜色:
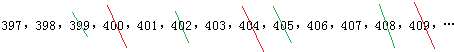
可见,剩下的第6个数是407,即取走1号棋子后,从剩下的最小号数,第181枚棋子的编号是407.
解答:解:第一圈取走:3000÷3=1000,
余下:3000-1000=2000,
第二圈取走:2000÷3=666…2,余数是2,最后取走了2000-2=1998,第1999、2000枚没有取走,
第三圈取得第一枚就是1号;共取走1000+666+1=1667(枚),
剩下3000-1667=1333(枚),
每18个一循环,18个数去掉10个,剩下8个.拿走1后,剩下的最小编号是2,从2数第181枚,就是从1数第182枚,
182÷8=22…6,
22×18=396,
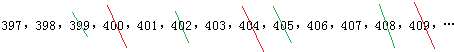
剩下的第6个数是407;
答:圆周上还有1333枚棋子;在圆周上剩下的棋子中,从编号最小一枚棋子开始数,第181枚棋子的编号是407.
余下:3000-1000=2000,
第二圈取走:2000÷3=666…2,余数是2,最后取走了2000-2=1998,第1999、2000枚没有取走,
第三圈取得第一枚就是1号;共取走1000+666+1=1667(枚),
剩下3000-1667=1333(枚),
每18个一循环,18个数去掉10个,剩下8个.拿走1后,剩下的最小编号是2,从2数第181枚,就是从1数第182枚,
182÷8=22…6,
22×18=396,
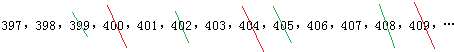
剩下的第6个数是407;
答:圆周上还有1333枚棋子;在圆周上剩下的棋子中,从编号最小一枚棋子开始数,第181枚棋子的编号是407.
点评:解决此题的关键是发现每18个一循环,18个数去掉10个,剩下8个.

练习册系列答案
相关题目