题目内容
 如图三角形AOB是等腰直角三角形,AO=AB=10厘米,半圆ADB的 为AB,以O为圆心的扇形OAC的半径为AO=10厘米,求图中阴影部分的面积.(保留?)
如图三角形AOB是等腰直角三角形,AO=AB=10厘米,半圆ADB的 为AB,以O为圆心的扇形OAC的半径为AO=10厘米,求图中阴影部分的面积.(保留?)
解:以AB为直径的半圆面积:
3.14×(10÷2)2÷2,
=3.14×52÷2,
=3.14×25÷2,
=78.5÷2,
=39.25(平方厘米);?
以O为圆心,AO为半径的扇形OAC的面积是:
3.14×102×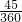 ,
,
=3.14×100× ,
,
=314× ,
,
=39.25(平方厘米);
等腰直角△OAB的面积是:
10×10÷2,
=100÷2,
=50(平方厘米);
所以整个阴影部分面积是:
39.52+39.52-50,
=78.5-50,
=28.5(平方厘米);
答:图中阴影部分的面积是28.5平方厘米.
分析:由题意可知:阴影部分面积可以看成是以AB为直径的半圆面积加上以O为圆心,AO为半径的扇形OAC的面积减去直角三角形OAB的面积
点评:解答此题的关键是明白:扇形所在圆的面积为扇形面积的8倍,且半圆的面积加上扇形的面积减去直角三角形的面积即可.
3.14×(10÷2)2÷2,
=3.14×52÷2,
=3.14×25÷2,
=78.5÷2,
=39.25(平方厘米);?
以O为圆心,AO为半径的扇形OAC的面积是:
3.14×102×
 ,
,=3.14×100×
 ,
,=314×
 ,
,=39.25(平方厘米);
等腰直角△OAB的面积是:
10×10÷2,
=100÷2,
=50(平方厘米);
所以整个阴影部分面积是:
39.52+39.52-50,
=78.5-50,
=28.5(平方厘米);
答:图中阴影部分的面积是28.5平方厘米.
分析:由题意可知:阴影部分面积可以看成是以AB为直径的半圆面积加上以O为圆心,AO为半径的扇形OAC的面积减去直角三角形OAB的面积
点评:解答此题的关键是明白:扇形所在圆的面积为扇形面积的8倍,且半圆的面积加上扇形的面积减去直角三角形的面积即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 调入乙队后两队人数相等,原来甲队人数比乙队
调入乙队后两队人数相等,原来甲队人数比乙队


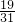 的分子、分母同时加上一个数后,结果等于
的分子、分母同时加上一个数后,结果等于 ,所加的这个数是________.
,所加的这个数是________.