题目内容
盒子中装有8个红球和8个白球,任意摸出1个球,是红球的可能性是________,至少摸出________个球,才能保证至少有2个球的颜色相同.
 3
3分析:(1)先用“8+8”求出盒子中球的个数,求出摸一个球,摸到红球的可能性,根据可能性的求法:即求一个数是另一个数的几分之几用除法解答;
(2)求至少摸出几个球,就可保证至少有两个球的颜色相同,把球的颜色种类看作“抽屉”,根据抽屉原理可知:要保证少有两个球的颜色相同.至少应摸出2+1=3个.
解答:(1)8÷(8+8)=
 ,
,(2)要保证少有两个球的颜色相同.至少应摸出2+1=3个.
答:是红球的可能性是
 ,至少摸出3个球,才能保证至少有2个球的颜色相同;
,至少摸出3个球,才能保证至少有2个球的颜色相同;故答案为:
 ,3.
,3.点评:解答此类题用到的知识点:(1)求一个数是另一个数的几分之几用除法解答,进而得出结论;
(2)找出把谁看作“抽屉个数”,把谁看作“物体个数”,然后根据抽屉原理解答即可.

练习册系列答案
相关题目
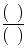 ,至少摸出( )个球,就可保证其中至少有2个球的颜色相同。
,至少摸出( )个球,就可保证其中至少有2个球的颜色相同。