题目内容
 如图圆的直径BC=8厘米,ABCD是平行四边形,线段AB=7厘米,DE=3.5厘米,∠BCD=30度,求阴影部分的周长和面积.( π取3)
如图圆的直径BC=8厘米,ABCD是平行四边形,线段AB=7厘米,DE=3.5厘米,∠BCD=30度,求阴影部分的周长和面积.( π取3)
解:连接OD,
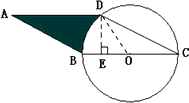
阴影部分的面积为:
8×3.5-[(8÷2)×3.5÷2+ ×3×
×3×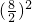 ],
],
=28-[4×3.5+8],
=28-[14+8],
=28-22,
=6(平方厘米);
阴影部分的周长为:
7+8+( ×3×8),
×3×8),
=15+4,
=19(厘米);
答:阴影部分的面积为6平方厘米,周长为19厘米.
分析:根据平行四边形对边平行且相等的特征,AD=BC=8厘米,可连接OD,得到等腰三角形CDO,∠BOD=60°,阴影部分的面积等于平行四边形的面积减弧BD所对应的圆的面积再减去三角形CDO的面积,其中DE为三角形CDO的高,弧BD所对应的圆心角为60°,占整个圆心角的 ,所以弧BD所对应的面积就占整个圆面积的
,所以弧BD所对应的面积就占整个圆面积的 ,根据平行四边形的面积公式、圆的面积公式和三角形的面积公式进行计算即可得到答案;阴影部分的周长等于线段AB加线段AD加弧BD的长,因为弧BD所对应的圆心角为60°,占整个圆心角的
,根据平行四边形的面积公式、圆的面积公式和三角形的面积公式进行计算即可得到答案;阴影部分的周长等于线段AB加线段AD加弧BD的长,因为弧BD所对应的圆心角为60°,占整个圆心角的 ,所以弧BD的长就占整个圆周长的
,所以弧BD的长就占整个圆周长的 ,根据圆的周长公式进行解答即可得到答案.
,根据圆的周长公式进行解答即可得到答案.
点评:解答此题的关键是连接OD,将平行四边形中的空白部分分为一个三角形和一个圆的 ,再根据平行四边形的面积公式、三角形的面积公式、圆的面积公式计算阴影部分的面积;根据弧BD所对应的圆心角为60°,占整个圆心角的
,再根据平行四边形的面积公式、三角形的面积公式、圆的面积公式计算阴影部分的面积;根据弧BD所对应的圆心角为60°,占整个圆心角的 ,所以弧BD的长就占整个圆周长的
,所以弧BD的长就占整个圆周长的 ,根据圆的周长公式进行计算即可.
,根据圆的周长公式进行计算即可.

阴影部分的面积为:
8×3.5-[(8÷2)×3.5÷2+
 ×3×
×3×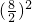 ],
],=28-[4×3.5+8],
=28-[14+8],
=28-22,
=6(平方厘米);
阴影部分的周长为:
7+8+(
 ×3×8),
×3×8),=15+4,
=19(厘米);
答:阴影部分的面积为6平方厘米,周长为19厘米.
分析:根据平行四边形对边平行且相等的特征,AD=BC=8厘米,可连接OD,得到等腰三角形CDO,∠BOD=60°,阴影部分的面积等于平行四边形的面积减弧BD所对应的圆的面积再减去三角形CDO的面积,其中DE为三角形CDO的高,弧BD所对应的圆心角为60°,占整个圆心角的
 ,所以弧BD所对应的面积就占整个圆面积的
,所以弧BD所对应的面积就占整个圆面积的 ,根据平行四边形的面积公式、圆的面积公式和三角形的面积公式进行计算即可得到答案;阴影部分的周长等于线段AB加线段AD加弧BD的长,因为弧BD所对应的圆心角为60°,占整个圆心角的
,根据平行四边形的面积公式、圆的面积公式和三角形的面积公式进行计算即可得到答案;阴影部分的周长等于线段AB加线段AD加弧BD的长,因为弧BD所对应的圆心角为60°,占整个圆心角的 ,所以弧BD的长就占整个圆周长的
,所以弧BD的长就占整个圆周长的 ,根据圆的周长公式进行解答即可得到答案.
,根据圆的周长公式进行解答即可得到答案.点评:解答此题的关键是连接OD,将平行四边形中的空白部分分为一个三角形和一个圆的
 ,再根据平行四边形的面积公式、三角形的面积公式、圆的面积公式计算阴影部分的面积;根据弧BD所对应的圆心角为60°,占整个圆心角的
,再根据平行四边形的面积公式、三角形的面积公式、圆的面积公式计算阴影部分的面积;根据弧BD所对应的圆心角为60°,占整个圆心角的 ,所以弧BD的长就占整个圆周长的
,所以弧BD的长就占整个圆周长的 ,根据圆的周长公式进行计算即可.
,根据圆的周长公式进行计算即可. 
练习册系列答案
相关题目
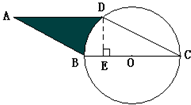 如图圆的直径BC=8厘米,ABCD是平行四边形,线段AB=7厘米,DE=3.5厘米,∠BCD=30度,求阴影部分的周长和面积.( π取3)
如图圆的直径BC=8厘米,ABCD是平行四边形,线段AB=7厘米,DE=3.5厘米,∠BCD=30度,求阴影部分的周长和面积.( π取3)