题目内容
9.按要求计算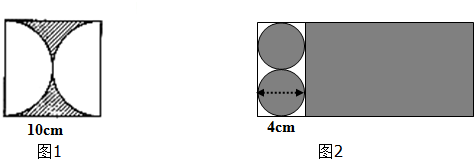
(1)求图1阴影部分的周长;
(2)图2是一个圆柱的表面展开图,求圆柱表面积.
分析 (1)阴影部分的周长等于直径10分米的圆的周长与两条正方形的边长之和;
(2)圆柱的底面直径是4厘米,可以先求出底面半径,根据圆的面积公式求出圆柱的底面积,再根据圆的周长公式求出圆柱的底面周长,也就是侧面展开图中长方形的长,观察图发现圆柱的高是两个底面直径的长度,由此求出圆柱的高也就是侧面展开图中长方形的宽,根据长方形的面积公式求出侧面积,进而求出表面积.
解答 解:(1)3.14×10+10×2
=31.4+20
=51.4(cm)
答:阴影部分的周长是51.4cm.
(2)3.14÷(4÷2)2×2
=3.14×4×2
=12.56×2
=25.12(平方厘米)
(3.14×4)×(4×2)
=12.56×8
=100.48(平方厘米)
25.12+100.48=125.6(平方厘米)
答:圆柱的表面积是125.6平方厘米.
点评 解决问题(1)注意分清楚阴影部分周长是由哪几部分构成的;问题(2)关键是找出圆柱的展开图中各部分的关系,正确运用公式求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.与81.8×2.4的乘积相等的算式是( )
| A. | 81.4×24 | B. | 0.818×240 | C. | 8.18×2.4 |
4.因为$\frac{1}{2}$-$\frac{1}{3}$=$\frac{1}{6}$,$\frac{1}{3}$-$\frac{1}{4}$=$\frac{1}{12}$,那么$\frac{1}{9}$-$\frac{1}{10}$=( )
| A. | $\frac{1}{90}$ | B. | $\frac{2}{19}$ | C. | $\frac{19}{90}$ |
18.整数a大于0,那么( )
| A. | a>$\frac{1}{a}$ | B. | a<$\frac{1}{a}$ | C. | a=$\frac{1}{a}$ | D. | a≥$\frac{1}{a}$ |
 如图是一个半径是5米的圆形花坛的平面图,现在设计师要在圆形花坛的周围修一条宽是1米的环形小路,请你帮他画出这条小路,并用阴影表示出来.并计算出环形小路的面积.
如图是一个半径是5米的圆形花坛的平面图,现在设计师要在圆形花坛的周围修一条宽是1米的环形小路,请你帮他画出这条小路,并用阴影表示出来.并计算出环形小路的面积.