题目内容
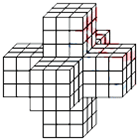 如图所示,用许多棱长为1厘米的小立方体粘合成一个实心的立体图形,那么该立体图形的体积和表面积分别为( )立方厘米和平方厘米.(注:该立体图形上下对称、左右对称、前后对称)
如图所示,用许多棱长为1厘米的小立方体粘合成一个实心的立体图形,那么该立体图形的体积和表面积分别为( )立方厘米和平方厘米.(注:该立体图形上下对称、左右对称、前后对称)| A、162,270 | B、189,324 | C、189,270 | D、162,324 |
分析:(1)根据题干,这个几何体的体积就是这些小正方体的体积之和,棱长1厘米的正方体的体积是1立方厘米,由此只要数出有几个小正方体就能求得这个几何体的体积;
(2)这个几何体的表面积就是露出正方体的面的面积之和,从上面看有45个面;从下面看有45个面;从前面看有45个面;从后面看有45个面;从左面看有45个面;从右面看有45个面.由此即可解决问题.
(2)这个几何体的表面积就是露出正方体的面的面积之和,从上面看有45个面;从下面看有45个面;从前面看有45个面;从后面看有45个面;从左面看有45个面;从右面看有45个面.由此即可解决问题.
解答:解:(1)这个几何体共有小正方体的个数为:3×3×3×7=189(个),
所以这个几何体的体积为:1×1×1×189=189(立方厘米).
(2)图中几何体露出的面有:45×6=270(个),
所以这个立体图形的表面积是:1×1×270=270(平方厘米).
答:该立体图形的体积是189立方厘米,表面积是270平方厘米.
故选:C.
所以这个几何体的体积为:1×1×1×189=189(立方厘米).
(2)图中几何体露出的面有:45×6=270(个),
所以这个立体图形的表面积是:1×1×270=270(平方厘米).
答:该立体图形的体积是189立方厘米,表面积是270平方厘米.
故选:C.
点评:此题考查了观察几何体的方法的灵活应用;抓住这个几何体的体积等于这些小正方体的体积之和;几何体的表面积是露出的小正方体的面的面积之和是解决此类问题的关键.

练习册系列答案
相关题目