Question

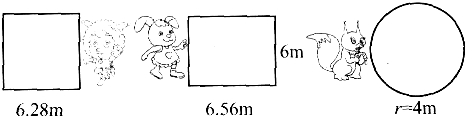
小山羊、小兔和小松鼠在草地上用篱笆各围了一块菜地（如下图）．

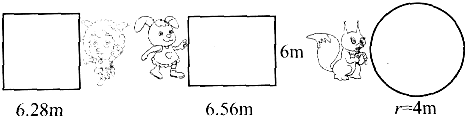
（1）它们各用了多少米长的篱笆？
（2）谁围的菜园面积最大，谁围的面积最小？你发现了什么？

Answer 1

解：（1）6.28×4=25.12（米），
（6.56+6）×2=25.12（米），
2×3.14×4=25.12（米），
答：它们用到篱笆的长都是25.12米；

（2）正方形面积：6.28×6.28=39.4384（平方米），
长方形的面积：6.56×6=39.36（平方米），
圆的面积：3.14×4²=50.24（平方米），
因为50.24＞39.4384＞39.36，
所以小松鼠围的面积最大，小兔围的面积最小，
发现：周长相等的长方形、正方形和圆形，圆形的面积最大；
答：小松鼠围的面积最大，小兔围的面积最小，发现：周长相等的长方形、正方形和圆形，圆形的面积最大．
分析：（1）求各用了多少米的篱笆，即求长方形、正方形和圆的周长，根据：长方形的周长=（长+宽）×2，正方形的周长=边长×4，圆的周长=2πr，分别进行解答；
（2）根据：长方形的面积=长×宽，正方形的面积=边长×边长，圆的面积=πr²，分别求出长方形、正方形、圆的面积，然后比较即可．
点评：此题考查了长方形、正方形、圆的周长和面积公式的灵活运用，明确周长相等的长方形、正方形和圆形，圆形的面积最大．