题目内容
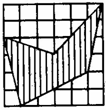 一个小正方形的面积是1平方厘米,阴影部分的面积是
一个小正方形的面积是1平方厘米,阴影部分的面积是14
14
平方厘米.分析:由题意结合图形可知,原图是由36个边长为1厘米的小正方形组成的一个边长为6厘米的大正方形,因此大正方形的面积是36平方厘米,阴影部分的面积=大正方形的面积-周围空白区域的面积,要求周围空白区域的面积,可以如下图所示,把其分割为5个规则的图形,①是上底、下底和高分别为2厘米、3厘米、3厘米的梯形;②是底和高都是3厘米的三角形;③是底和高分别是1厘米、4厘米的三角形;④是上底、下底和高分别为1厘米、5厘米、2厘米的梯形;⑤是底和高分别为1厘米、4厘米的三角形;利用梯形及三角形的面积公式即可解决.


解答:解:36-[(2+3)×3÷2+3×3÷2+1×4÷2+(1+5)×2÷2+1×4÷2],
=36-[7.5+4.5+2+6+2]
=36-22
=14(平方厘米);
答:阴影部分的面积是14平方厘米.
故答案为:14.
=36-[7.5+4.5+2+6+2]
=36-22
=14(平方厘米);
答:阴影部分的面积是14平方厘米.
故答案为:14.
点评:组合图形的面积,一般是转化为规则图形的面积的和或差解决问题,注意给学生渗透转化的数学思想方法.

练习册系列答案
相关题目

 图中每一个小正方形的面积是1平方厘米,请在图中绘制出面积为6平方厘米的长方形、平行四边形、三角形和梯形.
图中每一个小正方形的面积是1平方厘米,请在图中绘制出面积为6平方厘米的长方形、平行四边形、三角形和梯形.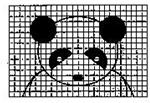 如图熊猫图案的阴影部分的面积是
如图熊猫图案的阴影部分的面积是 如图,一个长方形被分割成5个正方形,已知长方形的面积为120平方厘米,一个小正方形的面积是
如图,一个长方形被分割成5个正方形,已知长方形的面积为120平方厘米,一个小正方形的面积是