题目内容
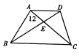 在梯形ABCD中S△ABE=12平方厘米,AE=
在梯形ABCD中S△ABE=12平方厘米,AE= EC,则梯形的面积SABCD=________平方厘米.
EC,则梯形的面积SABCD=________平方厘米.
48
分析:三角形ABE和三角形BCE的高相等,由AE= EC即AE:EC=2:3,根据三角形等高时,两个三角形底的比就是面积的比,据此可得三角形ABE和三角形BCE的面积比是2:3,S△ABE=12平方厘米,据此可求出三角形BCE的面积,因为三角形ABE和三角形DCE的面积相等,即都等于12平方厘米,三角形DCE和三角形ADE是等高的三角形,因为它们底的比AE:EC=2:3,所以三角形ADE和三角形DCE的面积比是2:3,三角形DCE的面积是12平方厘米已求出,则三角形ADE的面积可求,最后面积SABCD=S△ABE+S△BCE+S△DCE+S△ADE,即可求得.
EC即AE:EC=2:3,根据三角形等高时,两个三角形底的比就是面积的比,据此可得三角形ABE和三角形BCE的面积比是2:3,S△ABE=12平方厘米,据此可求出三角形BCE的面积,因为三角形ABE和三角形DCE的面积相等,即都等于12平方厘米,三角形DCE和三角形ADE是等高的三角形,因为它们底的比AE:EC=2:3,所以三角形ADE和三角形DCE的面积比是2:3,三角形DCE的面积是12平方厘米已求出,则三角形ADE的面积可求,最后面积SABCD=S△ABE+S△BCE+S△DCE+S△ADE,即可求得.
解答:由AE= EC即AE:EC=2:3,S△ABE=12平方厘米,
EC即AE:EC=2:3,S△ABE=12平方厘米,
S△BCE=12÷2×3=18平方厘米,
S△ABE=S△DCE=12平方厘米,
三角形ADE和三角形DCE的面积比是:2:3,
则:S△ADE=12÷3×2=8平方厘米,
所以SABCD=S△ABE+S△BCE+S△DCE+S△ADE=12+18+12+8=48平方厘米;
故答案为:48.
点评:本题主要利用三角形等高时,两个三角形底的比就是面积的比,这一特性求出另一三角形的面积.
分析:三角形ABE和三角形BCE的高相等,由AE=
 EC即AE:EC=2:3,根据三角形等高时,两个三角形底的比就是面积的比,据此可得三角形ABE和三角形BCE的面积比是2:3,S△ABE=12平方厘米,据此可求出三角形BCE的面积,因为三角形ABE和三角形DCE的面积相等,即都等于12平方厘米,三角形DCE和三角形ADE是等高的三角形,因为它们底的比AE:EC=2:3,所以三角形ADE和三角形DCE的面积比是2:3,三角形DCE的面积是12平方厘米已求出,则三角形ADE的面积可求,最后面积SABCD=S△ABE+S△BCE+S△DCE+S△ADE,即可求得.
EC即AE:EC=2:3,根据三角形等高时,两个三角形底的比就是面积的比,据此可得三角形ABE和三角形BCE的面积比是2:3,S△ABE=12平方厘米,据此可求出三角形BCE的面积,因为三角形ABE和三角形DCE的面积相等,即都等于12平方厘米,三角形DCE和三角形ADE是等高的三角形,因为它们底的比AE:EC=2:3,所以三角形ADE和三角形DCE的面积比是2:3,三角形DCE的面积是12平方厘米已求出,则三角形ADE的面积可求,最后面积SABCD=S△ABE+S△BCE+S△DCE+S△ADE,即可求得.解答:由AE=
 EC即AE:EC=2:3,S△ABE=12平方厘米,
EC即AE:EC=2:3,S△ABE=12平方厘米,S△BCE=12÷2×3=18平方厘米,
S△ABE=S△DCE=12平方厘米,
三角形ADE和三角形DCE的面积比是:2:3,
则:S△ADE=12÷3×2=8平方厘米,
所以SABCD=S△ABE+S△BCE+S△DCE+S△ADE=12+18+12+8=48平方厘米;
故答案为:48.
点评:本题主要利用三角形等高时,两个三角形底的比就是面积的比,这一特性求出另一三角形的面积.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
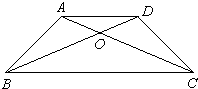
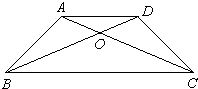 在梯形ABCD中,上底长5厘米,下底长10厘米,S△BOC=20平方厘米,则梯形ABCD的面积是
在梯形ABCD中,上底长5厘米,下底长10厘米,S△BOC=20平方厘米,则梯形ABCD的面积是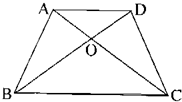 在梯形ABCD中,上底长4厘米,下底长8厘米,S△COD=9平方厘米,梯形ABCD面积是
在梯形ABCD中,上底长4厘米,下底长8厘米,S△COD=9平方厘米,梯形ABCD面积是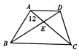 在梯形ABCD中S△ABE=12平方厘米,AE=
在梯形ABCD中S△ABE=12平方厘米,AE=