题目内容
5.小明用红、橙、黄、绿、青、蓝、紫七种颜色依次在一张纸条上涂色,第一次用红色涂了纸条的$\frac{1}{2}$,第二次用橙色涂了剩下的$\frac{1}{2}$,第三次用黄色又涂了剩下的$\frac{1}{2}$.照这样涂完n次后,还剩这张纸条的$\frac{1}{{2}^{n}}$没有涂色;第40次涂色时用的是青.分析 第一次用红色涂了纸条的$\frac{1}{2}$,还剩下纸条的$\frac{1}{2}$,第二次用橙色涂了剩下的$\frac{1}{2}$,还剩下纸条的$\frac{1}{2}$×$\frac{1}{2}$,第三次用黄色又涂了剩下的$\frac{1}{2}$,还剩下纸条的$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{2}$,…以此类推涂完n次后,还剩这张纸条的$\frac{1}{2}$×$\frac{1}{2}$×…×$\frac{1}{2}$=$\frac{1}{{2}^{n}}$没有涂色;
因为七种颜色依次不断循环,用40÷7看余数,找出对应的颜色即可.
解答 解:第一次用红色涂了纸条的$\frac{1}{2}$,还剩下纸条的$\frac{1}{2}$,
第二次用橙色涂了剩下的$\frac{1}{2}$,还剩下纸条的$\frac{1}{2}$×$\frac{1}{2}$,
第三次用黄色又涂了剩下的$\frac{1}{2}$,还剩下纸条的$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{2}$,
…
涂完n次后,还剩这张纸条的$\frac{1}{2}$×$\frac{1}{2}$×…×$\frac{1}{2}$=$\frac{1}{{2}^{n}}$.
40÷7=5…5
所以第40次涂色时用的是青.
故答案为:$\frac{1}{{2}^{n}}$,青.
点评 找出计算与循环的规律是解决问题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
17.直接写出得数:
| 5.4+8.5= | 150×6= | 6.78+0.23= | 10-6.5+3.5= |
| 7.5×100= | 60×50= | 287-199= | 0.3×125×8= |
| 1-0.09= | 927÷9= | 60÷100= | 6.3×99+6.3= |

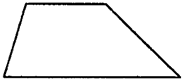 在如图的梯形里画一条线段,把它分割成一个平行四边形和一个三角形,并在图中找出一个钝角,量出度数并在图上标出来.
在如图的梯形里画一条线段,把它分割成一个平行四边形和一个三角形,并在图中找出一个钝角,量出度数并在图上标出来.