题目内容
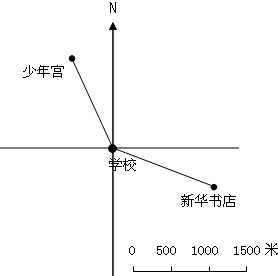 如图是县城某区域平面图.
如图是县城某区域平面图.
①这幅图的比例尺用数值表示是________.
②少年宫在学校________方向________米处.
③新华书店在学校________方向________米处.
④图书馆在学校北偏东45°方向1500米处,体育馆在学校南偏西70°方向750米处,在图中表示出他们的位置.
1:50000 西北 1000 东南 1250
分析:(1)依据比例尺的意义,即“比例尺= ”,即可将线段比例尺改为数值比例尺.
”,即可将线段比例尺改为数值比例尺.
(2)少年宫应该在学校的西北方向,量出二者的图上距离,再据“实际距离=图上距离÷比例尺”即可求得两地的距离.
(3)新华书店在学校的东南方向,量出二者的图上距离,再据“实际距离=图上距离÷比例尺”即可求得两地的距离.
(4)弄清楚方向和角度,依据“图上距离=实际距离×比例尺”即可求得它们与学校的图上距离,从而标出其位置.
解答:(1)因为500米=50000厘米,
则1厘米:50000厘米=1:50000;
答:这幅图的数值比例尺是1:50000.
(2)少年宫在学校的西北方向,其图上距离约为2厘米,
则少年宫距离学校:2÷ =100000(厘米)=1000米;
=100000(厘米)=1000米;
答:少年宫在学校西北方向1000米处.
(3)新华书店在学校的东南方向,其图上距离约为2.5厘米,
则新华书店距离学校:2.5÷ =125000(厘米)=1250米;
=125000(厘米)=1250米;
答:新华书店在学校东南方向1250米处.
(4)因为1500米=150000厘米,750米=75000厘米
则图书馆与学校的图上距离:150000× =3(厘米),
=3(厘米),
体育馆与学校的图上距离:75000× =1.5(厘米);
=1.5(厘米);
故如图标注:
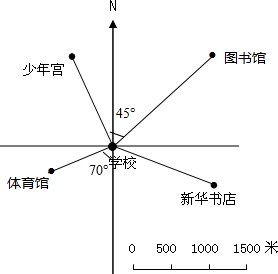
故答案为:1:50000;西北、1000;东南、1250;
点评:此题主要考查比例尺的意义以及图上距离、实际距离和比例尺的关系,解答时要注意单位的换算,并看清角度和方向再进行标注.
分析:(1)依据比例尺的意义,即“比例尺=
 ”,即可将线段比例尺改为数值比例尺.
”,即可将线段比例尺改为数值比例尺.(2)少年宫应该在学校的西北方向,量出二者的图上距离,再据“实际距离=图上距离÷比例尺”即可求得两地的距离.
(3)新华书店在学校的东南方向,量出二者的图上距离,再据“实际距离=图上距离÷比例尺”即可求得两地的距离.
(4)弄清楚方向和角度,依据“图上距离=实际距离×比例尺”即可求得它们与学校的图上距离,从而标出其位置.
解答:(1)因为500米=50000厘米,
则1厘米:50000厘米=1:50000;
答:这幅图的数值比例尺是1:50000.
(2)少年宫在学校的西北方向,其图上距离约为2厘米,
则少年宫距离学校:2÷
 =100000(厘米)=1000米;
=100000(厘米)=1000米;答:少年宫在学校西北方向1000米处.
(3)新华书店在学校的东南方向,其图上距离约为2.5厘米,
则新华书店距离学校:2.5÷
 =125000(厘米)=1250米;
=125000(厘米)=1250米;答:新华书店在学校东南方向1250米处.
(4)因为1500米=150000厘米,750米=75000厘米
则图书馆与学校的图上距离:150000×
 =3(厘米),
=3(厘米),体育馆与学校的图上距离:75000×
 =1.5(厘米);
=1.5(厘米);故如图标注:

故答案为:1:50000;西北、1000;东南、1250;
点评:此题主要考查比例尺的意义以及图上距离、实际距离和比例尺的关系,解答时要注意单位的换算,并看清角度和方向再进行标注.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
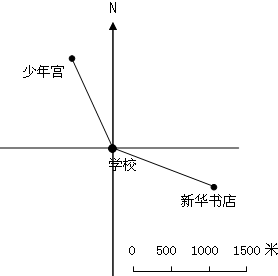 如图是县城某区域平面图.
如图是县城某区域平面图.