题目内容
18. 如图,在三角形ABC中,点D、E、F分别为AB、BC、CA延长线的点,且$\frac{AD}{AB}$=2;$\frac{BE}{BC}$=3;$\frac{CF}{AC}$=4,三角形ABC的面积为1,则三角形DEF的面积为20.5.
如图,在三角形ABC中,点D、E、F分别为AB、BC、CA延长线的点,且$\frac{AD}{AB}$=2;$\frac{BE}{BC}$=3;$\frac{CF}{AC}$=4,三角形ABC的面积为1,则三角形DEF的面积为20.5.
分析 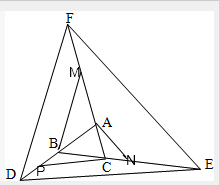
过点B作线段DE的平行线交线段AF与点M,过点A作线段EF的平行线交线段CE与点N,过点C作线段DE的平行线交线段DB与点P,因为$\frac{AD}{AB}$=2;$\frac{BE}{BC}$=3;$\frac{CF}{AC}$=4,所以MA:AC=1.5:1,CN:BC=1:2,PB:AB=1:2,根据等高的三角形的面积之比等于底的比,即可求得三角形AMB的面积=2三角形ABC的面积=2×1=2,三角形ANC的面积=三角形ABC面积的一半=1÷2=0.5,三角形CBP的面积=三角形ABC面积的一半=1÷2=0.5,再根据相似三角形面积的比等于相似比的平方求得:三角形AMB的面积:三角形ADF的面积=(1:2)2,得出三角形ADF的面积=8,同理可得:三角形CEF的面积=16×0.5=8,三角形DBE的面积=9×0.5=4.5,故此三角形AEF的面积=8+8+4.5=20.5,据此解答即可.
解答 解:如图: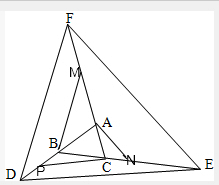
过点B作线段DE的平行线交线段AF与点M
过点A作线段EF的平行线交线段CE与点N
过点C作线段DE的平行线交线段DB与点P
因为:
且$\frac{AD}{AB}$=2;$\frac{BE}{BC}$=3;$\frac{CF}{AC}$=4
所以:
M:DF=AB:AD=1:2
AN:EF=CA:CF=1:4
PC:DB=BC:BE=1:3
MA:AC=1.5:1,CN:BC=1:2,PB:AB=1:2
根据等高的三角形面积之比等于它们底的比,所以:
三角形AMB的面积=2三角形ABC的面积=2×1=2
三角形ANC的面积=三角形ABC面积的一半=1÷2=0.5
三角形CBP的面积=三角形ABC面积的一半=1÷2=0.5
所以:
三角形AMB的面积:三角形ADF的面积=(1:2)2
三角形ADF的面积=8
同理可得:
三角形CEF的面积=16×0.5=8
三角形DBE的面积=9×0.5=4.5
而:
三角形AEF的面积
=三角形ADF的面积+三角形CEF的面积+三角形DBE的面积
=8+8+4.5
=20.5
答:三角形DEF的面积为20.5
故答案为:20.5.
点评 考查了利用三角形相似及其等高的三角形的面积之间的关系,搞清楚它们之间的关系是关键.

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案| 660÷3= | 12×20= | 77÷7= | 70×40= | 100÷5÷2= |
| 30×23= | 903÷3= | 34×20= | 240÷30= | 450÷(3×3)= |
| 7.8-0.4= | 8.3+6.7= | 1-0.4= | 4.2+0.5= | 1-0.5-0.2= |


 如图是六(1)班是同学喜欢的饮料的统计图.
如图是六(1)班是同学喜欢的饮料的统计图.