题目内容
右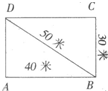 图是一个道路图.甲、乙两人在A地同时出发,甲每分钟走24米,沿着A-B-D-A-B-D…行走;乙每分钟走14米,沿着A-B-C-D-A-B-C-D行走.问两人出发后第一次在________相遇?(两人同时到达同一地点叫做相遇)
图是一个道路图.甲、乙两人在A地同时出发,甲每分钟走24米,沿着A-B-D-A-B-D…行走;乙每分钟走14米,沿着A-B-C-D-A-B-C-D行走.问两人出发后第一次在________相遇?(两人同时到达同一地点叫做相遇)
A
分析:由图可知,甲行一周的距离是:40+50+30=120(米),乙行了一周的距离是:(40+30)×2=140(米).然后由距离÷速度=时间,求出甲乙各行一周所需时间,再根据时间求出他们第一次相遇的地点即可.
解答:甲行一周所需时间为:
(40+50+30)÷24
=120÷24,
=5(分钟);
乙行一周所需时间为:
(40+30)×2÷44
=140÷2,
=10(分钟).
10÷5=2.
即甲每行两周,乙行一周.当甲行完第二周,乙行完第一周时,他们第一次相遇于A点.
故答案为:A点.
点评:由两人的速度及所行的路程,求出两人行完一周所用时间的比是完成本题的关键.
分析:由图可知,甲行一周的距离是:40+50+30=120(米),乙行了一周的距离是:(40+30)×2=140(米).然后由距离÷速度=时间,求出甲乙各行一周所需时间,再根据时间求出他们第一次相遇的地点即可.
解答:甲行一周所需时间为:
(40+50+30)÷24
=120÷24,
=5(分钟);
乙行一周所需时间为:
(40+30)×2÷44
=140÷2,
=10(分钟).
10÷5=2.
即甲每行两周,乙行一周.当甲行完第二周,乙行完第一周时,他们第一次相遇于A点.
故答案为:A点.
点评:由两人的速度及所行的路程,求出两人行完一周所用时间的比是完成本题的关键.

练习册系列答案
相关题目
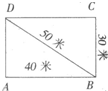 图是一个道路图.甲、乙两人在A地同时出发,甲每分钟走24米,沿着A-B-D-A-B-D…行走;乙每分钟走14米,沿着A-B-C-D-A-B-C-D行走.问两人出发后第一次在
图是一个道路图.甲、乙两人在A地同时出发,甲每分钟走24米,沿着A-B-D-A-B-D…行走;乙每分钟走14米,沿着A-B-C-D-A-B-C-D行走.问两人出发后第一次在