题目内容
【题目】某市为迎接“国家义务教育均衡发展”综合评估，市教育行政部门在全市范围内随机抽取了
所学校，并组织专家对两个必检指标进行考核评分.其中
分别表示“学校的基础设施建设”和“学校的师资力量”两项指标，根据评分将每项指标划分为
(优秀)、
(良好)、
(及格）三个等级，调查结果如表所示.例如：表中“学校的基础设施建设”指标为
等级的共有
所学校.已知两项指标均为
等级的概率为0.21.
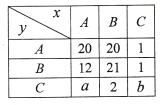
（1）在该样本中，若“学校的基础设施建设”优秀率是0.4，请填写下面
列联表，并根据列联表判断是否有
的把握认为“学校的基础设施建设”和“学校的师资力量”有关；
（2）在该样本的“学校的师资力量”为
等级的学校中，若
，记随机变量
，求
的分布列和数学期望.
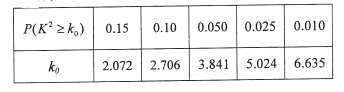
附表:
【答案】(1)答案见解析;(2)答案见解析.
【解析】试题分析：（1）由
，得
，由
，得
，由
得
，由此可得列联表，利用列联表数据根据公式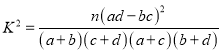
，求得
，与临界值比较即可得结果；（2）
的可能取值为
，根据古典概型概率公式求出各随机变量对应的概率，从而可得分布列，进而利用期望公式可得
的数学期望.
试题解析：（1）依题意得
，得
，由
，得
由
得
因为
，
所以没有
的把握认为“学校的基础设施建设”和“学校的师资力量”有关.
（2）
，得到满足条件的
有： 
故
的分布列为
故
练习册系列答案
浙江名校名师金卷系列答案
相关题目
