题目内容
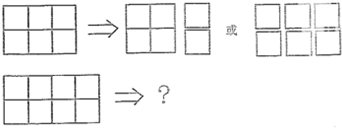
 现有一个3×4的长方形,现在任意横着切2刀,竖着切4刀,把长方形分成了15个小长方形,求这15个小长方形的周长之和是
现有一个3×4的长方形,现在任意横着切2刀,竖着切4刀,把长方形分成了15个小长方形,求这15个小长方形的周长之和是54
54
?分析:观察发现,每横着切一刀,那么长方形就增加了两条长为4的边,即周长和增加4×2=8,而每竖着切一刀,那么长方形就增加了两条长度为3的边,即周长和增加3×2=6.
用原长方形的周长加横切增加的周长,再加竖切增加的周长,就是周长之和.据此解答.
用原长方形的周长加横切增加的周长,再加竖切增加的周长,就是周长之和.据此解答.
解答:解:原长方形的周长:
2×(3+4),
=2×7,
=14,
横切后增加的周长:
4×2×2=16,
竖切增加的周长:
3×2×4=24.
周长之和是:
14+16+24=54.
答:周长之和是54.
故答案为:54.
2×(3+4),
=2×7,
=14,
横切后增加的周长:
4×2×2=16,
竖切增加的周长:
3×2×4=24.
周长之和是:
14+16+24=54.
答:周长之和是54.
故答案为:54.
点评:这15个小长方形中任何一个的周长我们都求不出,如果从局部出发,是不可能求出来的.因此我们要从整体出发去考虑.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 一种游戏机的“方块”游戏中共有七种图形:
一种游戏机的“方块”游戏中共有七种图形: