题目内容
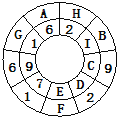
【题目】如图,在两个圆环内英文字母区域分别填入数字1~9,使得任何两个相邻区域内(有公共边的区域)的数字的差(大数减小数)至少是2,那么三位数![]() = .
= .
【答案】833
【解析】
试题分析:根据题干中已知数字的特点,奔着使任何两个相邻区域内(有公共边的区域)的数字的差(大数减小数)至少是2,进行分析讨论,明确各个数字的位置,即可解答问题.
解:(1)先看内圈:已知数字是1、2、6、7、9;根据数字位置特点可知,C可以是3、4、5;E可以是3、4、5;D和I不能为3和4,只能是5和8;所以C和E只能是3和4;又因为D和I必有5,所以C不能是4,则C=3,E=4,D=8,I=5;
(2)再看外圈:已知数字是1、2、6、9;根据数字位置特点可知,5只能在H,4只能在G,3只能在B,7只能在F,8只能是A,
所以可得:A=8,B=3,C=3,
所以这个三位数是833.
故答案为:833.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目