题目内容
2.自然数按约数的个数的多少分类,可以分为( )| A. | 偶数和奇数 | B. | 合数、素数、1 | C. | 合数和奇数 | D. | 合数、素数和1 |
分析 质数又称素数是指一个大于1的自然数,除了1和它本身两个因数外,再也没有其它的因数;合数是指一个大于1的自然数,除了1和它本身两个因数外,还有其它的因数;1只有1个因数就是它本身,所以1既不是质数,也不是合数.由此可知全体自然数按约数的个数分质数、合数和1三类.
解答 解:全体自然数按约数的个数分为三类:
①有1个因数的,即1;
②有2个因数的,即质数;
③有3个或3个以上因数的,即合数.
故选:D.
点评 此题考查全体自然数按约数的个数分几类,解答此题要明确质数和合数的概念.

练习册系列答案
相关题目
12.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是V+F-E=2;
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是20;
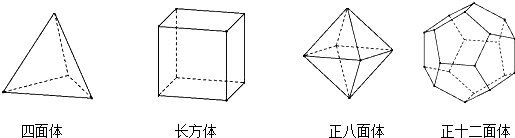
| 多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
| 四面体 | 4 | 4 | |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 8 | 12 | |
| 正十二面体 | 20 | 12 | 30 |
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是V+F-E=2;
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是20;
