题目内容
在正方形里分别作一个最大的圆,根据下面的条件完成表格.
| 正方形边长 | 1cm | 2cm | 3cm |
| 正方形面积 | |||
| 圆的面积 | |||
| 圆面积占正方形的% |
②如果一个正方形的面积是200平方厘米,在其中作的最大圆的面积应当是________平方厘米.
正方形内圆的面积占它所在的正方形的面积的百分比值是相等 157
分析:(1)正方形内最大的圆的直径等于正方形的边长,由此利用正方形和圆的面积公式计算即可完成表格;
(2)根据上述计算可得,圆的面积占正方形的面积的百分比是不变的;由此利用正方形的面积乘圆占正方形的面积的百分比即可解答.
解答:(1)当正方形的边长为1厘米时,
正方形的面积是1×1=1(平方厘米),
圆的面积是:π× =0.785(平方厘米),
=0.785(平方厘米),
则圆面积占正方形的面积的:0.785÷1=78.5%;
当正方形的边长为2厘米时,
正方形的面积是2×2=4(平方厘米),
圆的面积是:π× =3.14(平方厘米),
=3.14(平方厘米),
则圆面积占正方形的面积的:3.14÷4=78.5%;
正方形的边长为3厘米时,
正方形的面积是3×3=9(平方厘米),
圆的面积是:π×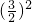 =7.065(平方厘米),
=7.065(平方厘米),
则圆面积占正方形的面积的:7.065÷9=78.5%;
由此即可完成表格如下所示,通过表格发现是:正方形内圆的面积占它所在的正方形的面积的百分比值是相等的.

(2)200×78.5%=157(平方厘米),
答:面积为200平方厘米的正方形内最大的圆的面积是157平方厘米.
故答案为:正方形内圆的面积占它所在的正方形的面积的百分比值是相等;157.
点评:此题主要考查正方形内最大的圆的特点,得出结论:正方形内最大的圆的面积占所在的正方形的面积的78.5%.
分析:(1)正方形内最大的圆的直径等于正方形的边长,由此利用正方形和圆的面积公式计算即可完成表格;
(2)根据上述计算可得,圆的面积占正方形的面积的百分比是不变的;由此利用正方形的面积乘圆占正方形的面积的百分比即可解答.
解答:(1)当正方形的边长为1厘米时,
正方形的面积是1×1=1(平方厘米),
圆的面积是:π×
 =0.785(平方厘米),
=0.785(平方厘米),则圆面积占正方形的面积的:0.785÷1=78.5%;
当正方形的边长为2厘米时,
正方形的面积是2×2=4(平方厘米),
圆的面积是:π×
 =3.14(平方厘米),
=3.14(平方厘米),则圆面积占正方形的面积的:3.14÷4=78.5%;
正方形的边长为3厘米时,
正方形的面积是3×3=9(平方厘米),
圆的面积是:π×
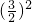 =7.065(平方厘米),
=7.065(平方厘米),则圆面积占正方形的面积的:7.065÷9=78.5%;
由此即可完成表格如下所示,通过表格发现是:正方形内圆的面积占它所在的正方形的面积的百分比值是相等的.

(2)200×78.5%=157(平方厘米),
答:面积为200平方厘米的正方形内最大的圆的面积是157平方厘米.
故答案为:正方形内圆的面积占它所在的正方形的面积的百分比值是相等;157.
点评:此题主要考查正方形内最大的圆的特点,得出结论:正方形内最大的圆的面积占所在的正方形的面积的78.5%.

练习册系列答案
相关题目
