Question

【题目】2016 年崇明区政府投资 8 千万元启动休闲体育新乡村旅游项目．规划从 2017 年起，在今后的若干年内，每年继续投资 2 千万元用于此项目.2016 年该项目的净收入为 5 百万元，并预测在相当长的年份里，每年的净收入均为上一年的基础上增长．记 2016 年为第 1 年， 为第 1 年至此后第 年的累计利润（注：含第 年，累计利润=累计净收入﹣累计投入，单位：千万元），且当 为正值时，认为该项目赢利．

（1）试求 的表达式；

（2）根据预测，该项目将从哪一年开始并持续赢利？请说明理由．

Answer 1

【答案】(1) ；（2）.

【解析】试题分析：（1）由题意知，第一年至此后第年的累计投入为（千万元），第年至此后第年的累计净收入为，利用等比数列数列的求和公式可得；（2）由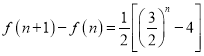，利用指数函数的单调性即可得出.

试题解析：（1）由题意知，第1年至此后第n（n∈N*）年的累计投入为8+2（n﹣1）=2n+6（千万元），

第1年至此后第n（n∈N*）年的累计净收入为+×+×+…+×

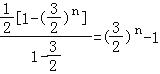=（千万元）．

∴f（n）=﹣（2n+6）=﹣2n﹣7（千万元）．

（2）方法一：∵f（n+1）﹣f（n）=[﹣2（n+1）﹣7]﹣[﹣2n﹣7]=[﹣4]，

∴当n≤3时，f（n+1）﹣f（n）＜0，故当n≤4时，f（n）递减；

当n≥4时，f（n+1）﹣f（n）＞0，故当n≥4时，f（n）递增．

又f（1）=﹣＜0，f（7）=≈5×﹣21=﹣＜0，f（8）=﹣23≈25﹣23=2＞0．

∴该项目将从第8年开始并持续赢利．

答：该项目将从2023年开始并持续赢利；

方法二：设f（x）=﹣2x﹣7（x≥1），则f′（x）=，

令f'（x）=0，得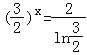=≈=5，∴x≈4．

从而当x∈[1，4）时，f'（x）＜0，f（x）递减；

当x∈（4，+∞）时，f'（x）＞0，f（x）递增．

又f（1）=﹣＜0，f（7）=≈5×﹣21=﹣＜0，f（8）=﹣23≈25﹣23=2＞0．

∴该项目将从第8年开始并持续赢利．

答：该项目将从2023年开始并持续赢利．