题目内容
3. 把一张长12厘米,宽8厘米的长方形方格纸(如图,每小格边长1厘米)裁成同样大的正方形(边长为整厘米数).如果要求纸没有剩余,符合要求的正方形边长有几种情况?最大是多少厘米?一共可以裁出多少个这样的正方形?(先求一求,再画一画.)
把一张长12厘米,宽8厘米的长方形方格纸(如图,每小格边长1厘米)裁成同样大的正方形(边长为整厘米数).如果要求纸没有剩余,符合要求的正方形边长有几种情况?最大是多少厘米?一共可以裁出多少个这样的正方形?(先求一求,再画一画.)
分析 裁成同样大小,且没有剩余,就是裁成的小正方形的边长是12和8的公因数,要求面积最大的正方形就是以12和8的最大公因数为小正方形的边长,然后用长方形纸片的长和宽分别除以小正方形的边长,就是长方形纸片的长边最少可以裁几个,宽边最少可以裁几个,最后把它们乘起来即可.
解答 解:
12=2×3×3,
8=2×2×2,
所以1,2,4是12和8的公因数
所以符合要求的正方形边长有3种情况;
所以12和8的最大公因数是2×2=4;即小正方形的边长是4厘米,
长方形纸片的长边可以分;12÷4=3(个),
宽边可以分:8÷4=2(个),
一共可以分成:2×3=6(个);
答:符合要求的正方形边长有3种情况;裁出的正方形边长最大是4厘米,一共可以裁出6个这样的正方形.
点评 本题关键是理解:裁成同样大小,且没有剩余,就是裁成的小正方形的边长是12和8的公因数;用到的知识点:两个数的公有质因数连乘积是最大公约数,两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
18.48□是一个既是2的倍数,又是3的倍数的数,□里可以填( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
8.观察图,跳绳的有30人,跑步的大约有( )人.
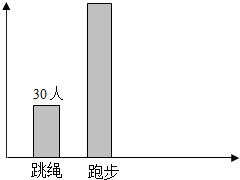

| A. | 60 | B. | 90 | C. | 120 | D. | 160 |
15.从( )看,下面三个物体的形状完全相同的.


| A. | 上面和正面 | B. | 上面和侧面 | C. | 侧面和正面 | D. | 以上答案都对 |