Question

19．如图，OC=2AO，阴影部分的面积为14cm²，求梯形的面积．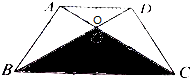

Answer 1

分析 △ABO和△BCO是等高的两个三角形，因为OC=2AO，所以△ABO的面积等于△BCO面积的一半；同理得到△CDO的面积是△BCO面积的一半；△ADO和△CDO是等高的两个三角形，因为OC=2AO，所以△ADO的面积是△CDO面积的一半，然后再用空白部分的面积加阴影部分的面积进行计算即可．

解答 解：因为OC=2AO，
△ABO的面积=14÷2=7（平方厘米）
△CDO的面积=14÷2=7（平方厘米）
△ADO的面积=7÷2=3.5（平方厘米）
梯形的面积=7+7+3.5+14=31.5（平方厘米）
答：梯形的面积是31.5平方厘米．

点评 解答此题的关键是利用等高是两个三角形，它们底边的比等于它们的面积比．