题目内容
甲、乙两个班的学生同时从学校出发去距学校54千米的海洋公园.学校只有1辆汽车,它的速度是45千米/时,这辆汽车恰好能坐1个班的学生,为了让两个班的学生尽快同时到达公园,采取甲班学生先步行,乙班学生先乘车,汽车到达中途某地点时,乙班学生下车继续步行,汽车返回接甲班步行的学生.如果两个班学生步行速度都是5千米/时,那么两个班的学生用最短的时间同时到达公园用多少小时?(上、下车所用时间不计)
解:由分析和根据时间一定,路程的比就等于速度的比可得:
AB:(AC+BC)=5:45=1:9,
则AB:2BC=1:8,
所以AB:BC=1:4;
在C点甲班下车走路,汽车返回接乙班,然后汽车与甲班同时到达公园可得:(BC+CD):CD=45:5=9:1,
则2BC:CD=8:1,
所以BC:CD=4:1;
由AB:BC=1:4和BC:CD=4:1可得AB:BC:CD=1:4:1,
所以A点到C点的距离是:54×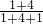 =45(千米),
=45(千米),
A点到B点的距离与C点到D点的距离都是:54×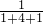 =9(千米);
=9(千米);
甲班从A点到D点所用的时间:45÷45+9÷5
=1+1.8
=2.8(小时),
答:两个班的学生用最短的时间同时到达公园用2.8小时.
分析:最短时间到达,只需要甲班乘坐汽车与乙班走路同时到达某公园设,甲班先坐车,乙班走路,当汽车把甲班送到C点,甲班学生下车走路,汽车返回在B点处接乙班的学生,根据时间一定,路程的比就等于速度的比:简单画图如:
AB:(AC+BC)=5:45=1:9,则AB:2BC=1:8,所以AB:BC=1:4;在C点甲班下车走路,汽车返回接乙班,然后汽车与甲班同时到达公园可得:(BC+CD):CD=45:5=9:1,
则2BC:CD=8:1,所以BC:CD=4:1;由AB:BC=1:4和BC:CD=4:1可得AB:BC:CD=1:4:1,所以A点到C点的距离是:54×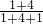 =45(千米),A点到B点的距离与C点到D点的距离都是:54×
=45(千米),A点到B点的距离与C点到D点的距离都是:54×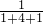 =9(千米);然后根据路程除以速度等于时间,求出甲班从A点到D点所用的时间,就是两个班的学生用最短的时间同时到达公园用时间.
=9(千米);然后根据路程除以速度等于时间,求出甲班从A点到D点所用的时间,就是两个班的学生用最短的时间同时到达公园用时间.
点评:解答此题根据时间一定,路程的比就等于速度的比求出各部分的比,进而求出甲班坐车和步行的路程,然后依据路程除以速度等于时间,两个班的学生用最短的时间同时到达公园用时间.
AB:(AC+BC)=5:45=1:9,
则AB:2BC=1:8,
所以AB:BC=1:4;
在C点甲班下车走路,汽车返回接乙班,然后汽车与甲班同时到达公园可得:(BC+CD):CD=45:5=9:1,
则2BC:CD=8:1,
所以BC:CD=4:1;
由AB:BC=1:4和BC:CD=4:1可得AB:BC:CD=1:4:1,
所以A点到C点的距离是:54×
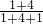 =45(千米),
=45(千米),A点到B点的距离与C点到D点的距离都是:54×
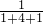 =9(千米);
=9(千米);甲班从A点到D点所用的时间:45÷45+9÷5
=1+1.8
=2.8(小时),
答:两个班的学生用最短的时间同时到达公园用2.8小时.
分析:最短时间到达,只需要甲班乘坐汽车与乙班走路同时到达某公园设,甲班先坐车,乙班走路,当汽车把甲班送到C点,甲班学生下车走路,汽车返回在B点处接乙班的学生,根据时间一定,路程的比就等于速度的比:简单画图如:

AB:(AC+BC)=5:45=1:9,则AB:2BC=1:8,所以AB:BC=1:4;在C点甲班下车走路,汽车返回接乙班,然后汽车与甲班同时到达公园可得:(BC+CD):CD=45:5=9:1,
则2BC:CD=8:1,所以BC:CD=4:1;由AB:BC=1:4和BC:CD=4:1可得AB:BC:CD=1:4:1,所以A点到C点的距离是:54×
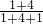 =45(千米),A点到B点的距离与C点到D点的距离都是:54×
=45(千米),A点到B点的距离与C点到D点的距离都是:54×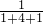 =9(千米);然后根据路程除以速度等于时间,求出甲班从A点到D点所用的时间,就是两个班的学生用最短的时间同时到达公园用时间.
=9(千米);然后根据路程除以速度等于时间,求出甲班从A点到D点所用的时间,就是两个班的学生用最短的时间同时到达公园用时间.点评:解答此题根据时间一定,路程的比就等于速度的比求出各部分的比,进而求出甲班坐车和步行的路程,然后依据路程除以速度等于时间,两个班的学生用最短的时间同时到达公园用时间.

练习册系列答案
相关题目