题目内容
用数字卡片 各2张,能组成________个不同的六位数.
各2张,能组成________个不同的六位数.
90
分析:先确定最高位十万位上的数是2,则万位上有3种选择,再分别将剩下的数位上的可能选择利用树状图列举出来,计算出一共有多少种方法;因为十万位上还可能是3或4,方法和2在首位时方法一样,所以用2在首位的方法数再乘3即可.
解答:如图所示:
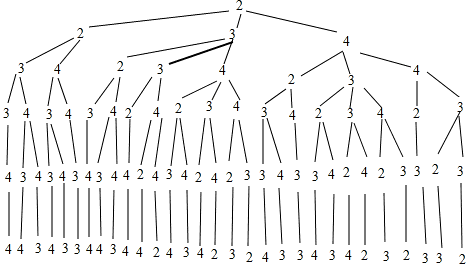
2在首位时的方法一共有30种方法,则一共有30×3=90(种).
答:能组成90个不同的六位数.
故答案为:90.
点评:解决本题主要借助树状图来解答,根据2在首位的排列方法,得出3、4在首位时的方法一样,进而得出结论.
分析:先确定最高位十万位上的数是2,则万位上有3种选择,再分别将剩下的数位上的可能选择利用树状图列举出来,计算出一共有多少种方法;因为十万位上还可能是3或4,方法和2在首位时方法一样,所以用2在首位的方法数再乘3即可.
解答:如图所示:

2在首位时的方法一共有30种方法,则一共有30×3=90(种).
答:能组成90个不同的六位数.
故答案为:90.
点评:解决本题主要借助树状图来解答,根据2在首位的排列方法,得出3、4在首位时的方法一样,进而得出结论.

练习册系列答案
相关题目
 各2张,能组成
各2张,能组成