题目内容
甲、乙两车分别从A、B两地同时出发相向而行,出发时,甲和乙的速度比是4:3,相遇后,甲的速度增加10%,乙的速度增加20%,这样,当甲到达B地时,乙离A地还有17千米,那么A、B两地相距多少千米?
解:4+4×10%,
=4+0.4,
=4.4,
3+3×20%,
=3+0.6,
=3.6,
4.4:3.6=11:9,
3+4=7,
17÷(
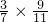 ),
),
=17÷(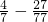 ),
),
=17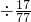 ,
,
=77(千米),
答:A、B两地相距77千米.
分析:根据出发时,甲和乙的速度比是4:3,和相遇后,甲的速度增加10%,乙的速度增加20%,可得:相遇后两人的速度比是(4+4×10%):(3+3×20%)=11:9,把两地间的距离看作单位“1”,当相遇后,甲到达B地时,甲就行驶了全程的 =
= ,根据时间一定,路程和速度成正比可得:相遇后乙就行驶了甲相遇后行驶路程的
,根据时间一定,路程和速度成正比可得:相遇后乙就行驶了甲相遇后行驶路程的 ,求出相遇后乙行驶的路程占总路程的量,然后根据相遇地点距A站的距离是全程的
,求出相遇后乙行驶的路程占总路程的量,然后根据相遇地点距A站的距离是全程的 ,进而求出乙车再相遇后行驶的量比相遇地点距A站的距离少的量,也就是17千米占两地间距离的分率,依据分数除法意义即可解答.
,进而求出乙车再相遇后行驶的量比相遇地点距A站的距离少的量,也就是17千米占两地间距离的分率,依据分数除法意义即可解答.
点评:本题属于比较困难的应用题,关键是依据时间一定,路程和速度成正比,求出相遇后乙行驶的路程占总路程的量,进而求出17千米占两地间距离的分率.
=4+0.4,
=4.4,
3+3×20%,
=3+0.6,
=3.6,
4.4:3.6=11:9,
3+4=7,
17÷(

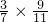 ),
),=17÷(
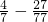 ),
),=17
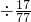 ,
,=77(千米),
答:A、B两地相距77千米.
分析:根据出发时,甲和乙的速度比是4:3,和相遇后,甲的速度增加10%,乙的速度增加20%,可得:相遇后两人的速度比是(4+4×10%):(3+3×20%)=11:9,把两地间的距离看作单位“1”,当相遇后,甲到达B地时,甲就行驶了全程的
 =
= ,根据时间一定,路程和速度成正比可得:相遇后乙就行驶了甲相遇后行驶路程的
,根据时间一定,路程和速度成正比可得:相遇后乙就行驶了甲相遇后行驶路程的 ,求出相遇后乙行驶的路程占总路程的量,然后根据相遇地点距A站的距离是全程的
,求出相遇后乙行驶的路程占总路程的量,然后根据相遇地点距A站的距离是全程的 ,进而求出乙车再相遇后行驶的量比相遇地点距A站的距离少的量,也就是17千米占两地间距离的分率,依据分数除法意义即可解答.
,进而求出乙车再相遇后行驶的量比相遇地点距A站的距离少的量,也就是17千米占两地间距离的分率,依据分数除法意义即可解答.点评:本题属于比较困难的应用题,关键是依据时间一定,路程和速度成正比,求出相遇后乙行驶的路程占总路程的量,进而求出17千米占两地间距离的分率.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目