题目内容
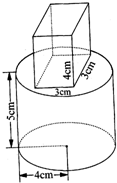 如图,由一个长方体木块和一个圆柱体木块粘合而成的模型,长方体的长、宽、高分别是3厘米、3厘米、4厘米,圆柱体的高是5厘米,底面半径是4厘米.这个模型的体积和表面积分别是多少?
如图,由一个长方体木块和一个圆柱体木块粘合而成的模型,长方体的长、宽、高分别是3厘米、3厘米、4厘米,圆柱体的高是5厘米,底面半径是4厘米.这个模型的体积和表面积分别是多少?分析:由于上面的长方体和下面的圆柱体粘合在一起,所以它的表面积等于长方体的表面积加上圆柱的表面积减去长方体的两个底面积.也就是上面的长方体只计算4个侧面的面积;
它的体积等于长方体和圆柱体的体积之和,根据长方体的体积公式:v=abh,圆柱的体积公式:v=sh,据此列式解答.
它的体积等于长方体和圆柱体的体积之和,根据长方体的体积公式:v=abh,圆柱的体积公式:v=sh,据此列式解答.
解答:解:体积:
3×3×4+3.14×42×5,
=36+3.14×16×5,
=36+251.2,
=287.2(立方厘米);
表面积:
3×4×4+2×3.14×4×5+3.14×42×2,
=48+125.6+3.14×16×2,
=48+125.6+100.48,
=274.08(平方厘米);
答:这个模型的体积是287.2立方厘米,表面积是274.08平方厘米.
3×3×4+3.14×42×5,
=36+3.14×16×5,
=36+251.2,
=287.2(立方厘米);
表面积:
3×4×4+2×3.14×4×5+3.14×42×2,
=48+125.6+3.14×16×2,
=48+125.6+100.48,
=274.08(平方厘米);
答:这个模型的体积是287.2立方厘米,表面积是274.08平方厘米.
点评:此题主要考查长方体、圆柱体的表面积公式、体积公式的灵活运用,解答关键是明白:上面的长方体和下面的圆柱体粘合在一起,长方体的下底面不外露,圆柱的上底面也被长方体盖住了同样的面积,所以上面的长方体只计算4个侧面的面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
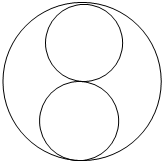 如图是由一个大圆和两个相等的小圆所组成的图形.小圆直径是20厘米.大圆的半径是
如图是由一个大圆和两个相等的小圆所组成的图形.小圆直径是20厘米.大圆的半径是 根据图中数据填空.
根据图中数据填空.
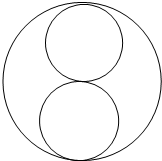 如图是由一个大圆和两个相等的小圆所组成的图形.小圆直径是20厘米.大圆的半径是________厘米;它有________条对称轴.
如图是由一个大圆和两个相等的小圆所组成的图形.小圆直径是20厘米.大圆的半径是________厘米;它有________条对称轴.