题目内容
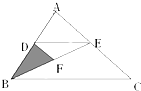
如图D、E、F是AB、AC、BE的中点,三角形ABE是三角形DBF的( )倍.

| A、4 | B、6 | C、8 | D、10 |
考点:组合图形的面积
专题:平面图形的认识与计算
分析:首先根据三角形的中位线定理证明△BDF∽△BAE,且相似比为1:2;再进一步根据相似三角形的面积比是相似比的平方进行求解.
解答:
解:因为点D、F分别是△ABE的三边AB、BE上的中点,
所以DF∥AE,DB=
AB.
所以△BDF∽△BAE,且相似比为1:4,
即:三角形ABE是三角形DBF的4倍.
故选:A.
所以DF∥AE,DB=
| 1 |
| 2 |
所以△BDF∽△BAE,且相似比为1:4,
即:三角形ABE是三角形DBF的4倍.
故选:A.
点评:此题考查了三角形的中位线定理、相似三角形的性质:相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目
下列各种图形不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
小明用圆片表示的数是314,小红用圆片表示的数是( )


| A、357 | B、537 |
| C、573 | D、737 |
68×99用简便方法计算是( )
| A、68×100+68×1 |
| B、68×100-68 |
| C、68×100+1 |
| D、68×100-1 |