题目内容
17.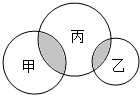 如图,甲圆和乙圆的面积之和是丙圆面积的$\frac{3}{5}$,甲圆内阴影部分面积占乙圆面积的$\frac{1}{2}$,甲圆内阴影部分面积占丙圆面积的$\frac{1}{8}$,那么甲、乙两圆面积的比是多少?
如图,甲圆和乙圆的面积之和是丙圆面积的$\frac{3}{5}$,甲圆内阴影部分面积占乙圆面积的$\frac{1}{2}$,甲圆内阴影部分面积占丙圆面积的$\frac{1}{8}$,那么甲、乙两圆面积的比是多少?
分析 设甲圆内阴影部分面积为k,则乙圆面积为k÷$\frac{1}{2}$=2k,丙圆面积为k÷$\frac{1}{8}$=8k,甲圆和乙圆的面积之和是丙圆面积的$\frac{3}{5}$,为8k×$\frac{3}{5}$=$\frac{24}{5}$k,甲圆面积为$\frac{24}{5}$k-2k=$\frac{14}{5}$k,再求甲、乙两圆面积的比即可.
解答 解:甲圆内阴影部分面积为k,则乙圆面积为k÷$\frac{1}{2}$=2k,
丙圆面积为k÷$\frac{1}{8}$=8k,
甲圆和乙圆的面积之和是丙圆面积的$\frac{3}{5}$,为8k×$\frac{3}{5}$=$\frac{24}{5}$k,
甲圆面积为$\frac{24}{5}$k-2k=$\frac{14}{5}$k,
$\frac{24}{5}$k:2k=$\frac{12}{5}$,
答:甲、乙两圆面积的比是$\frac{12}{5}$.
点评 本题考查了重叠问题,关键是设甲圆内阴影部分面积为k,把甲圆和乙圆的面积用k表示出来.

练习册系列答案
相关题目
8.每个篮球c元,实验小学购进10个,一共需要( )元.
| A. | c+10 | B. | c-10 | C. | 10c | D. | c÷10 |
5.
| 直接写出结果 1÷$\frac{1}{6}$= | 20×$\frac{2}{3}$= | $\frac{1}{3}$÷$\frac{3}{8}$= | $\frac{8}{21}$×$\frac{7}{16}$= |
| $\frac{3}{4}$+$\frac{1}{4}$= | $\frac{5}{6}$-$\frac{1}{6}$= | 2-$\frac{4}{5}$= | $\frac{1}{5}$+$\frac{1}{4}$= |
| $\frac{5}{7}$+$\frac{7}{5}$= | $\frac{5}{12}$×$\frac{4}{15}$= |
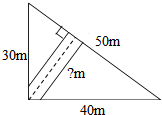 在一块直角三角形草坪上修一条垂直于斜边的小路(如图),这条小路长多少米?
在一块直角三角形草坪上修一条垂直于斜边的小路(如图),这条小路长多少米?