题目内容
有两根一样长的铁丝,一根围成长方形,一根围成圆,
圆
圆
的面积大.分析:本题可假设周长是多少,根据这两种几何图形的面积公式分别求得面积后进行比较即可.
解答:解:假设周长是628厘米,则圆的半径是100厘米,面积是31400平方厘米,
和它周长相等的长方形的面积是:长方形一条长和宽的和是628÷2=314,设这个长方形的长、宽分别为a、b:
取一些数字(10,304),(50,264),(100,214)…,
可以发现长方形的长和宽越接近,面积就越大,当长和宽相等时,也就是变成正方形了,
所以这个长方形的面积一定小于正方形的面积.
所以在周长相等的情况下,面积:圆>长方形.
故答案为:圆.
和它周长相等的长方形的面积是:长方形一条长和宽的和是628÷2=314,设这个长方形的长、宽分别为a、b:
取一些数字(10,304),(50,264),(100,214)…,
可以发现长方形的长和宽越接近,面积就越大,当长和宽相等时,也就是变成正方形了,
所以这个长方形的面积一定小于正方形的面积.
所以在周长相等的情况下,面积:圆>长方形.
故答案为:圆.
点评:考查了周长相同的图形在所有图形中,圆的面积最大,是一个经典题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,第二根截去
,第二根截去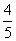 ,第二根截去
,第二根截去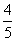 米,余下的部分
米,余下的部分