题目内容
如图所示，已知三角形ABC的面积是平行四边形CDEF面积的3倍，AD=2DC，且三角形BDE的面积为3，则三角形BEF的面积为________．
9平方厘米
分析：如图所示，连接CE，则S△BDE=S△CDE=
S平行四边形CDEF=3平方厘米，于是可以求出平行四边形的面积，再据“三角形ABC的面积是平行四边形CDEF面积的3倍”即可求出三角形ABC的面积，又因“AD=2DC”，则三角形DBC的面积=
S△ABC，而S△BEC=S△DBC+S△CDE-S△DBE，而三角形CEF的面积等于平行四边形的面积，
于是S△BEF=S△BEC+S△CEF，问题得解．
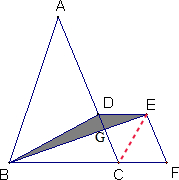
解答：连接CE，
则S△BDE=S△CDE=S平行四边形CDEF=3平方厘米，
S平行四边形DCFE=3×2=6（平方厘米）；
S△ABC=6×3=18（平方厘米），
又因AD=2DC，
则S△DBC=S△ABC=×18=6（平方厘米）；
S△BEC=3+6-3=6（平方厘米），
S△BEF=S△BEC+S△CEF，
=6+3，
=9（平方厘米）；
答：三角形BEF的面积为9平方厘米．
故答案为：9平方厘米．
点评：解答此题的关键是作出辅助线，先求出平行四边形的面积，进而求出三角形ABC的面积，于是即可逐步求解．
分析：如图所示，连接CE，则S△BDE=S△CDE=
S平行四边形CDEF=3平方厘米，于是可以求出平行四边形的面积，再据“三角形ABC的面积是平行四边形CDEF面积的3倍”即可求出三角形ABC的面积，又因“AD=2DC”，则三角形DBC的面积=S△ABC，而S△BEC=S△DBC+S△CDE-S△DBE，而三角形CEF的面积等于平行四边形的面积，于是S△BEF=S△BEC+S△CEF，问题得解．
解答：连接CE，
则S△BDE=S△CDE=
S平行四边形CDEF=3平方厘米，S平行四边形DCFE=3×2=6（平方厘米）；
S△ABC=6×3=18（平方厘米），
又因AD=2DC，
则S△DBC=
S△ABC=×18=6（平方厘米）；S△BEC=3+6-3=6（平方厘米），
S△BEF=S△BEC+S△CEF，
=6+3，
=9（平方厘米）；
答：三角形BEF的面积为9平方厘米．
故答案为：9平方厘米．
点评：解答此题的关键是作出辅助线，先求出平行四边形的面积，进而求出三角形ABC的面积，于是即可逐步求解．
练习册系列答案
相关题目
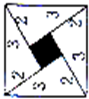在一次国际数学大会上，大会的会标如图所示．已知每个直角三角形的两条直角边都分别为2和3，求会标的面积．（单位：厘米）
如图所示，已知三角形ABC的面积是平行四边形CDEF面积的3倍，AD=2DC，且三角形BDE的面积为3，则三角形BEF的面积为
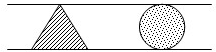如图所示，已知三角形的底边长10厘米，三角形面积是40平方厘米，那么圆的
如图所示，已知三角形的底边长10厘米，三角形面积是40平方厘米，那么圆的