题目内容
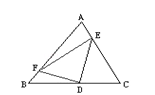
【题目】已知:AE=![]() AC,CD=
AC,CD=![]() BC,BF=
BC,BF=![]() AB,求三角形DEF的面积与三角形ABC的面积之比.
AB,求三角形DEF的面积与三角形ABC的面积之比.
【答案】61:120
【解析】
试题分析:可以先求出边上的3个小三角形与S△ABC的面积之间的关系:S△BDF=S△ABC×![]() ×
×![]() =
=![]() S△ABC,S△CDE=S△ABC×
S△ABC,S△CDE=S△ABC×![]() ×
×![]() =
=![]() S△ABC,S△AEF=S△ABC×
S△ABC,S△AEF=S△ABC×![]() ×
×![]() =
=![]() S△ABC,所以S△DEF=S△ABC﹣S△BDF﹣S△CDE﹣S△AEF=
S△ABC,所以S△DEF=S△ABC﹣S△BDF﹣S△CDE﹣S△AEF=![]() S△ABC,依此即可求解.
S△ABC,依此即可求解.
解:因为S△BDF=S△ABC×![]() ×
×![]() =
=![]() S△ABC,
S△ABC,
S△CDE=S△ABC×![]() ×
×![]() =
=![]() S△ABC,
S△ABC,
S△AEF=S△ABC×![]() ×
×![]() =
=![]() S△ABC,
S△ABC,
所以S△DEF=S△ABC﹣S△BDF﹣S△CDE﹣S△AEF=![]() S△ABC,
S△ABC,
答:三角形DEF的面积与三角形ABC的面积之比为61:120.

练习册系列答案
相关题目
【题目】下面是三年级学生喜欢的快餐情况统计表。
男生喜欢的快餐情况
种类 | 肯德基 | 德克士 | 麦当劳 | 必胜客 |
人数 | 12 | 9 | 15 | 8 |
女生喜欢的快餐情况
种类 | 肯德基 | 德克士 | 麦当劳 | 必胜客 |
人数 | 19 | 4 | 12 | 5 |
请你把调查的结果合成一个复式统计表。
| 肯德基 | 德克士 | 麦当劳 | 必胜客 |
男生 | ||||
女生 |
(1)男生中喜欢( )的人数最多,女生中喜欢( )的人数最多。
(2)三年级学生喜欢必胜客的共有( )人。
(3)西式快餐膳食结构不均衡,因此儿童不宜多吃。你对这些同学有什么建议呢?