题目内容
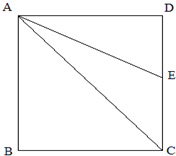 如图正方形的面积是36平方厘米,△ABC的面积比△ACE的面积大6平方厘米.DE的长度是多少厘米?
如图正方形的面积是36平方厘米,△ABC的面积比△ACE的面积大6平方厘米.DE的长度是多少厘米?分析:由题意可知:正方形的面积是36平方厘米,则正方形的边长为6厘米,三角形ABC的面积是正方形相等面积的一半,从而可以求出三角形ACE的面积,进而得出三角形ADE的面积,再据三角形的面积公式即可求出DE的长度.
解答:解:因为S正方形ABCD=36平方厘米,则S△ABC=18平方厘米,
所以S△ACE=18-6=12平方厘米,S△ADE=18-12=6平方厘米;
DE的长度为:6×2÷6=2(厘米);
答:DE的长度是2厘米.
所以S△ACE=18-6=12平方厘米,S△ADE=18-12=6平方厘米;
DE的长度为:6×2÷6=2(厘米);
答:DE的长度是2厘米.
点评:求出三角形ADE的面积,是解答本题的关键.

练习册系列答案
相关题目
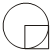 (2008?宝应县)如图正方形的面积是3平方米,圆的面积是
(2008?宝应县)如图正方形的面积是3平方米,圆的面积是 如图,以正方形OABC的边长为半径画一个圆,已知正方形的面积是3平方厘米,则圆的面积是
如图,以正方形OABC的边长为半径画一个圆,已知正方形的面积是3平方厘米,则圆的面积是 如图是两条互相垂直的直线,相交于点O.
如图是两条互相垂直的直线,相交于点O. 如图,以正方形OABC的边长为半径画一个圆,已知正方形的面积是3平方厘米,则圆的面积是________平方厘米.
如图,以正方形OABC的边长为半径画一个圆,已知正方形的面积是3平方厘米,则圆的面积是________平方厘米. 如图正方形的面积是3平方米,圆的面积是________平方米.
如图正方形的面积是3平方米,圆的面积是________平方米.